Момент силы относительно оси

Введем сначала понятие проекции силы на плоскость. Пусть даны сила 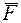и некоторая плоскость 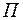. Опустим из начала и конца вектора силы перпендикуляры на эту плоскость (рис.16).

Проекцией силы на плоскость называется вектор 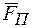, начало и конец которого (точки 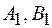) совпадают с проекциями начала и конца силы 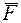(точки ).

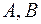Моментом силы 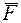относительно оси 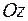называется алгебраическая величина 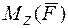, равная произведению модуля проекции 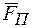силы 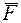на плоскость 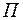, перпендикулярную к оси 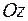(т.е. совпадающую с плоскостью 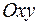), на кратчайшее расстояние 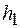от точки 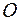пересечения оси с плоскостью до линии действия проекции силы (рис. 16).

Этому определению соответствует следующая зависимость.

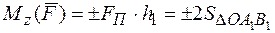. (17)

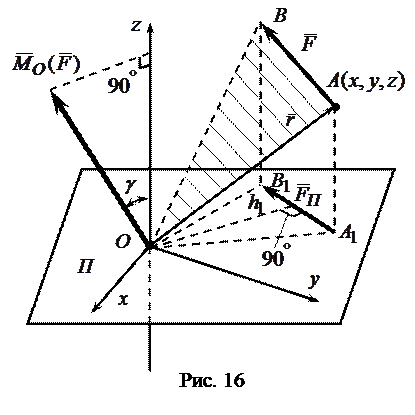Момент силы 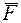относительно оси 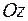считается положительным, если смотря с положительного конца этой оси, видим, что сила 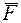стремится повернуть тело вокруг оси в направлении против хода часовой стрелки, и отрицательным, если - по ходу часовой стрелки.

Из определения 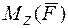следует, что момент силы относительно оси равен нулю в двух случаях:

1) Когда 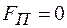, т.е. сила 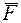параллельна оси ;

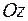2) когда 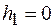, т.е. линия действия силы пересекает ось .

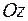Объединяя эти два случая, можно сказать, что момент силы относительно оси равен нулю, если сила и ось располагаются в одной плоскости.

Момент силы относительно точки связан с моментом силы относительно оси. Эту связь можно выразить следующей теоремой:

Проекция момента силы относительно точки на ось, проходящую через эту точку, равна моменту силы относительно этой оси.

Аналитически это теорема выражается следующей формулой:.

Поэтому окончательно имеем:

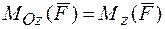. (18)