Основная теорема статики

Пусть на свободное твердое тело действует система сил 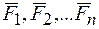, расположенных как угодно в пространстве и приложенных в точках 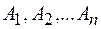(рис. 22). Выберем произвольно центр 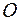и приведем все данные силы к этому центру (центру приведения). В результате получим силы 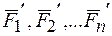,_,равные данным силам и приложенные в центре 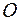и присоединенные пары 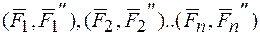. Моменты 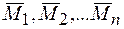этих присоединенных пар равны моментам данных сил относительно центра приведения:

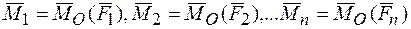. (24)

Складывая силы 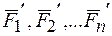, приложенные в центре 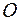по правилу многоугольника, получаем одну силу 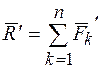. Так как силы 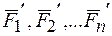равны данным силам 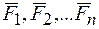, то можно записать

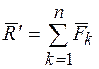. (25)

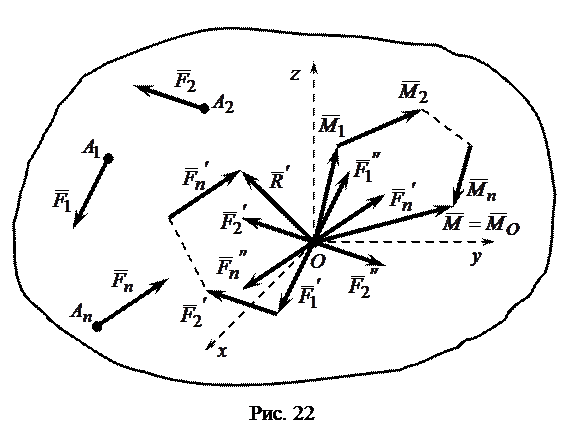Вектор 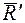, равный геометрической сумме всех сил системы, называется главным вектором системы сил.

Складывая присоединенные пары 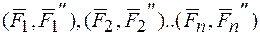, получим одну пару с моментом 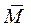, равным геометрической сумме моментов присоединенных пар.

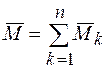. (26).

Учитывая (24), находим:

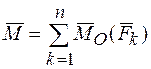, (27).

или 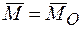, где

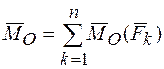. (28).

Вектор 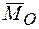, равный геометрической сумме моментов всех сил системы относительно центра приведения 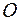, называется главным моментом системы сил относительно этого центра.

Таким образом, доказана основная теорема статики: произвольную систему сил, приложенную к свободному твердому телу, можно привести к одной силе, равной главному вектору системы сил, и приложенной в центре приведения и к одной паре с моментом, равным главному моменту этой системы относительно центра приведения.

Не следует отождествлять главный вектор 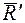c равнодействующей, так как он заменяет систему сил в сочетании с главным моментом, в то время как равнодействующая 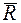, если она существует, одна заменяет систему сил.

При переносе центра приведения главный вектор не изменяется, а главный момент в общем случае изменяется.

Приведение произвольной системы сил к центру позволяет ответить на вопрос, являются ли две системы сил, приложенных к твердому телу, эквивалентными. Если при приведении этих двух систем к одному центру мы получим два равных главных вектора и главных момента, то можно утверждать, что такие две системы сил являются эквивалентными.

Случаи приведения произвольной системы сил к равнодействующей, к паре, к динаме изучаются студентами самостоятельно (см. [1],с. 94…97 или [2], с. 105…107).