Методика решения данной задачи полностью совпадает с той, которая использовалась при определении граничных условий для тангенциальных составляющих магнитного поля. Отличие состоит в том, что вместо второго уравнения Максвелла (закона полного тока) используется первое уравнение (закон электромагнитной индукции):

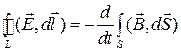
В соответствии с этим для малого контура, проведенного по границе раздела двух сред, будем иметь:
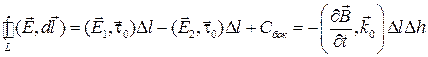 .
.
Проводя аналогичные рассуждения, получим
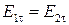 ,
,
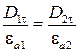 .
.
Таким образом, тангенциальные составляющие векторов напряженности электрического поля на границе раздела сред непрерывны, однако аналогичные составляющие векторов электрической индукции, вообще говоря, претерпевают разрыв.
Рассмотрим отдельно граничные условия в том случае, когда средой 2 является идеальный металл. Здесь, как уже известно, 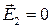 . Если бы внутри идеального металла существовала конечная напряженность электрического поля, то это привело бы к протеканию здесь бесконечно больших токов проводимости, и, как следствие, выделению бесконечно большого количества тепла, что противоречит физической сущности задачи. Таким образом, с учетом сказанного, граничное условие для идеального проводника принимает вид
. Если бы внутри идеального металла существовала конечная напряженность электрического поля, то это привело бы к протеканию здесь бесконечно больших токов проводимости, и, как следствие, выделению бесконечно большого количества тепла, что противоречит физической сущности задачи. Таким образом, с учетом сказанного, граничное условие для идеального проводника принимает вид
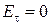 .
.
В соответствии с этим условием силовые линии электрического поля должны подходить к поверхности идеального металла по направлению нормали. Понятие «идеальный металл» является абстрактным, и на границе раздела с реальным металлом некоторая тангенциальная составляющая поля все же имеется. Однако, для многих случаев она весьма мала и в реальных задачах ее можно не учитывать.
 2015-10-22
2015-10-22 757
757








