2015-10-22
2345
Формулы комбинаторики составляют теоретическую базу при использовании классического определения вероятности, которое в прикладных задачах играет большую роль.
В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.
I. Перестановки.
Комбинации из n элементов, которые отличаются друг от друга только порядком элементов, называют перестановками. Обозначаются символом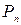 
.
, (
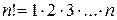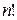– эн факториал)
Õ Пример. В ящике пять одинаковых пронумерованных кубиков. Наудачу по одному извлекают все кубики из ящика. Найти вероятность того, что номера извлеченных кубиков появятся в возрастающем порядке.
Решение. Обозначим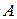 
– событие, состоящее в том, что номера извлеченных кубиков появятся в возрастающем порядке.
Благоприятствует событию 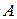только один исход, 
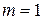(из всех возможных комбинаций номеров только одна с порядком возрастания номеров).
Общее число возможных исходов n – количество комбинаций из 
номеров, 
.
Искомая вероятность: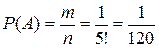 
.n
II. Размещения
Комбинации из n элементовпо k элементов, которые отличаются друг от друга или самими элементами, илипорядком элементов, называют размещениями.
Обозначаются символом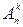 
– количество всех имеющихся элементов;
– количество элементов в каждой комбинации;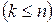 
.
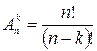
Õ Пример. Из пяти карточек с буквами О, П, Р, С, Т наугад одну за другой выбирают три и располагают в ряд в порядке появления. Какова вероятность того, что получится слово «ТОР»?
Решение. Обозначим 
– событие, состоящее в том, что получится слово «ТОР».
Благоприятствует событию только один исход,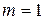 
(комбинация букв «ТОР»).
Общее число возможных исходов n равно числу способов, которыми можно отобрать 3 карточки из имеющихся 5, получая при этом комбинации букв отличающиеся либо самими буквами (СОР – ТОР), либо их порядком (РОТ – ОРТ). Оно определяется числом размещений из 5 элементов по 3:
.
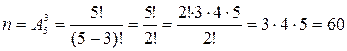Искомая вероятность:
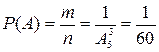.n
III. Сочетания
Сочетаниями называют все возможные комбинации из n элементовпо k элементов, которые отличаются друг от друга по крайней мере хотя бы одним элементом.
Обозначаются символом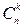 
– количество всех имеющихся элементов;
– количество элементов в каждой комбинации; .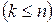
;
Õ Пример. В урне 5 белых и 4 красных шара. Из урны наудачу извлекают 3 шара. Найти вероятность того, что извлеченные шары – белые.
Решение. Обозначим – событие, состоящее в том, что все 3 шара будут белыми.
Всего в урне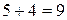 
шаров.
Общее число возможных элементарных исходов испытания n равно числу способов, которыми можно извлечь 3 шара из 9:
.
Число исходов благоприятствующих событию 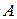исходов m равно числу способов, которыми можно отобрать 3 белых шара из имеющихся 5 белых:
.
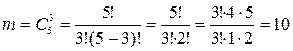Искомая вероятность равна:
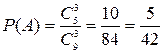.n
Õ Пример. В ящике имеется 11 одинаковых шаров. Причем 4 из них окрашены в синий цвет, а остальные белые. Наудачу извлекают 5 шаров. Найти вероятность того, что среди них 2 синих.
Решение. Обозначим 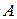– событие, состоящее в том, что среди извлеченных 5 шаров 2 синих.
Обще число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь 5 шаров из 11, т.е.
.
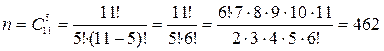Подсчитаем число исходов, благоприятствующих событию 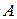: 2 синих шара можно взять из 4 имеющихся синих шаров 
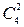способами; при этом остальные 
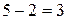шара должны быть белыми, взять же 3 белых шара из имеющихся 7 можно 
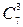способами. Следовательно, число благоприятствующих исходов равно:
.
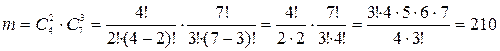Искомая вероятность:
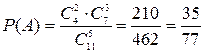.n
