2015-10-22
393
Вероятность является одним из основных понятий теории вероятностей. Существует несколько определений этого понятия. Рассмотрим определение, которое называют классическим.
Каждый из возможных результатов испытания, т.е. каждое событие, которое может наступить в испытании, назовем элементарным исходом.
Те элементарные исходы, при которых интересующее нас событие наступает, назовем благоприятствующими этому событию.
Вероятностью события А называют отношение числа благоприятствующих этому событию исходов 
к общему числу всех единственно возможных и равновозможных исходов испытания 
.
где 
– число элементарных исходов, благоприятствующих событию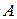 
;
– число всех возможных элементарных исходов испытания.
Для невозможного события 
;
Для достоверного события 
.
Следовательно, для произвольного случайного события 
Вероятность есть число, характеризующее возможность появления события. Обозначают вероятность 
, либо 
.
Õ Пример. В урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них – красные, 3 – синие и 1 – белый. Из урны наудачу вынимают один шар. Какова вероятность того, что извлеченный шар: а) красный; б) синий; в) белый?
|
|
|
Решение. а) Пусть событие 
– извлечен красный шар.
Число благоприятствующих событию 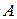исходов, 
(т.к. в урне 2 красных шара);
Число возможных исходов n= 6 (т.к. всего 6 шаров);
.
б) Пусть событие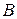 
– извлечен синий шар:
.
в) Пусть событие 
– извлечен белый шар:
n
Наряду с вероятностью, к основным понятиям теории вероятностей относится относительная частота.
Относительной частотой события называют отношение числа испытаний, в которых событие появилось, к общему числу фактически произведенных испытаний.
,
где – число появления события;
– общее число испытаний.
Вероятность вычисляют до опыта, а относительную частоту – после опыта.
Õ Пример. По цели произвели 24 выстрела, причем было зарегистрировано 19 попаданий. Относительная частота поражения цели 
n
