2015-10-22
2378
Если вероятность случайного события А вычисляется по условию, что событие В произошло, то такая вероятность называется условной.
Теорема умножения вероятностей зависимых событий.
Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго:
или 
.
Следствие: Вероятность совместного появления нескольких зависимых событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятности каждого последующего события вычисляются в предположении, что все предыдущие события уже появились.
.
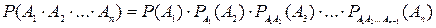где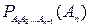 
– вероятность события 
, вычисленная в предположении, что события 
, 
, …, 
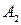наступили.
Õ Пример. В ящике 15 шаров: 7 синих и 8 желтых. Наудачу из ящика вынули один шар, а затем второй (не возвращая их обратно). Найти вероятность того, что первый из взятых шаров синий, а второй желтый.
Решение. Событие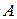 
– первый взятый шар синий. Вероятность события : 
.
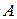Событие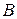 
– второй взятый шар желтый. Вероятность события 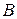, вычисленная в предположении, что первый шар синий (т.е. условная вероятность) равна: 
.
Искомая вероятность по теореме умножения вероятностей зависимых событий равна:
.n
