Вектор-столбец

называется собственным вектором квадратной матрицы 
 го порядка, соответствующим собственному значению
го порядка, соответствующим собственному значению  если он удовлетворяет матричному уравнению
если он удовлетворяет матричному уравнению
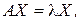 или
или 
Здесь  - единичная матрица
- единичная матрица  - го порядка, а 0 – нулевой вектор-столбец. При условии, что вектор
- го порядка, а 0 – нулевой вектор-столбец. При условии, что вектор 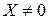 , получаем характеристическое уравнение для определения собственных значений
, получаем характеристическое уравнение для определения собственных значений 

Координаты собственного вектора  , соответствующего собственному значению
, соответствующего собственному значению  , являются решением системы уравнений
, являются решением системы уравнений

Собственный вектор определяется с точностью до постоянного множителя.
Пример. Определить собственные значения и собственные векторы матрицы 
Решение. Характеристическое уравнение для данной матрицы имеет вид:
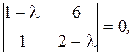 или
или 
откуда следует, что матрица  имеет два собственных значения
имеет два собственных значения  и
и  Собственный вектор
Собственный вектор  соответствующий
соответствующий  определяется из системы уравнений вида
определяется из системы уравнений вида
 , или
, или 
которая сводится к одному уравнению  Полагая
Полагая  получаем решение в виде
получаем решение в виде  Следовательно, первый собственный вектор есть
Следовательно, первый собственный вектор есть 
Второй собственный вектор 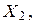 соответствующий собственному значению
соответствующий собственному значению 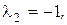 определяется из системы уравнений вида:
определяется из системы уравнений вида:

Эта система уравнений также сводится к одному уравнению  полагая
полагая  запишем ее решение в виде
запишем ее решение в виде 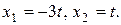 Следовательно, второй собственный вектор есть
Следовательно, второй собственный вектор есть 
Таким образом, матрица  имеет два собственных значения
имеет два собственных значения 
 и два собственных вектора, равных (с точностью до постоянного множителя)
и два собственных вектора, равных (с точностью до постоянного множителя) 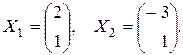
 2015-10-22
2015-10-22 286
286








