2015-10-22
320
Произведение вектора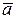 
на скалярный множитель l определяется по формуле l 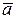= ( l а1, l а2, l а3).
Для двух векторов 
, 
их сумма и разность определяются по правилам:
Геометрически сумма и разность векторов строится как на рисунке:
|
|
Если точка О - начало координат, а М - точка с координатами (x, y, z), то вектор 
называется радиусом-вектором точки М.
Вектор 
с началом в точке А (x 1, y 1, z 1) и концом в точке В (x 2, y 2, z 2) в координатном виде записывается так: = 
.
Примеры.
а) В треугольнике АВС сторона АВ точками М и N разделена на три равные части: 
Найти вектор 
, если 
. Если построить треугольник и указанные вектора, то из геометрических правил сложения и вычитания легко получаются равенства 
т.е. 
. Так как 
, то 
Та-ким образом, 
б) Найти длину вектора 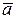= (10, 15, -30) и его направляющие косинусы.
По формулам (4.1) и (4.2) определяем
3) Найти вектор 
, если А (2, 1, 0) и В (3, 0, 5).
Из формулы для координат вектора имеем = (3-2, 0-1, 5-0) =
= (1, -1, 5).
