2015-10-22
318
Смешанным произведением трех векторов
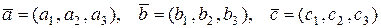называется число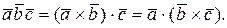 
Смешанное произведение обладает следующими свойствами:
а)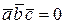 
, если все три вектора параллельны одной и той же плоскости (компланарны);
б)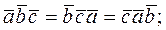 
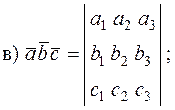
г) объем параллелепипеда, построенного на векторах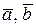 
и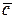 
, равен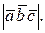 
Примеры.
а) Найти смешанное произведение векторов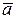 
=(5, 7, 2), 
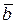= (1, -1, 1),
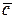= (2, 2, 1).
Из определения имеем
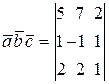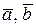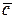= -5 + 14 + 4 + 4 - 10 - 7 = 0, т.е. вектора и компланарны.
б) Найти объем треугольной пирамиды с вершинами А (2, 2, 2),
В (4, 3, 3), С (4, 5, 4), D (5, 5, 6).
Из свойств смешанного произведения заключаем, что искомый объем равен
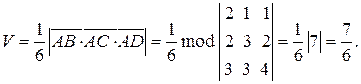
в) Вычислим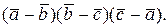 
Используя определение смешанного произведения и свойства векторного и скалярного произведений получаем
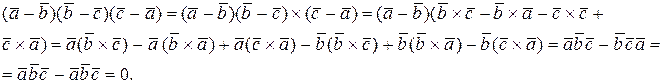
г) По координатам вершин пирамиды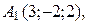 
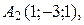
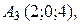
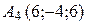найти: 1) длины ребер 
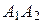и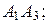 
2) угол между ребрам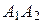и и 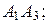3) площадь грани 
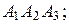4) объем пирамиды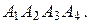 
Находим векторы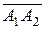 
и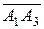 
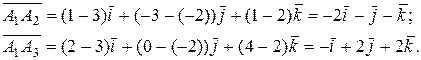
Длины векторов, т.е. длины ребер 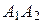и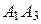 
, таковы:
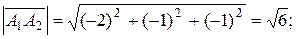
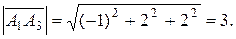
Скалярное произведение векторов 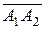и 
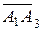равно
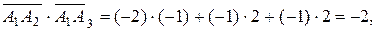
а косинус угла между ними:
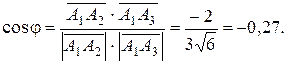
Отсюда следует, что 
- тупой угол, равный 
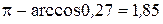(рад.) с точностью до 0,01. Это и есть искомый угол между ребрам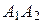и и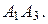 
Площадь грани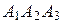 
равна половине площади параллелограмма, построенного на векторах 
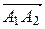и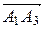 
, т.е. половине модуля векторного произведения этих векторов:
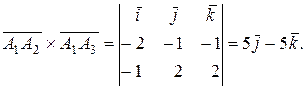
Следовательно, 
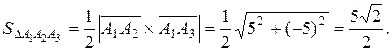
Объем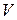 
пирамиды равен 
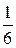объема параллелепипеда, построенного на векторах , , 
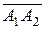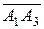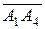. Вектор 
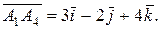Итак,
