2015-10-22
1818
Первую производную функции, заданной параметрически
находим по формуле 
.
Вторую производную удобно вычислять по формуле: 
.
Пример. Найти производную второго порядка функции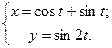 
Решение. Согласно формуле: 
Далее, 
.
Правило Лопиталя
Правило Лопиталя дает возможность раскрыть некоторые виды неопределенности, используя производную. Оно основывается на данной ниже теореме.
Теорема. Пусть функции 
и 
определенные и дифференцируемые в окружности точки 
, за исключением, возможно, самой точки а, и пусть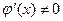 
в этой окружности. Если функции и являются одновременно бесконечно малыми или бесконечно большими при 
и к тому же существует отношение производных 
, то существует также предел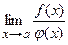 
, причем эти пределы равны между собой: = .
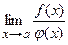Теорема справедлива и в том случае, когда 
. Если производные 
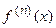и 
, n > 2, удовлетворяют тем же самым условиям, что и функции и , то =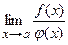 
.
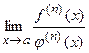Теорема дает возможность раскрыть неопределенность типа 
, которые будем называть основными. Чтобы раскрыть неопределенности типа 0, 
необходимо вначале привести их к основным и применить правило Лопиталя.
Пример.
1. 
2. 
= 
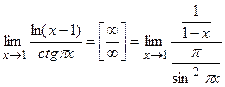3. 
4. 
5. 
Откуда, 
.
6. 
, действительно,
.
Напомним, что во многих случаях пользуемся равенством 
.
