Если у = f(u) и u = u(x), то есть 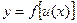 - сложная функция, причем функции у = f(u) и u = u(x) дифференцируемые, то
- сложная функция, причем функции у = f(u) и u = u(x) дифференцируемые, то 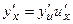 . Аргумент u часто называют промежуточной переменной. Это правило выполняется для сложной функции, которая имеет конечное число промежуточных аргументов. Если, например, у = f(u) и u = u(v), v=v(x), то
. Аргумент u часто называют промежуточной переменной. Это правило выполняется для сложной функции, которая имеет конечное число промежуточных аргументов. Если, например, у = f(u) и u = u(v), v=v(x), то 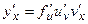 , если f(u), u(v) и v(x) - дифференцируемые.
, если f(u), u(v) и v(x) - дифференцируемые.
Формулы дифференцирования основных функций
1. 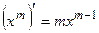 8.
8. 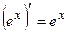
2. 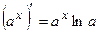 ,
, 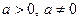 9.
9. 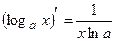 ,
, 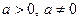
3. 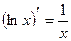 10.
10. 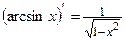
4. 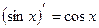 11.
11. 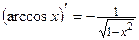
5. 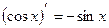
6. 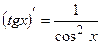 12.
12. 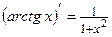
7. 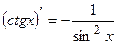 13.
13. 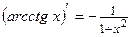
Примеры. Найти производные функций:
1. у = х4 – 2х3 + 3х + 1
Решение. Используя правила и формулы дифференцирования, получаем: 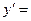 (х4 – 2х3 + 3х + 1)' =
(х4 – 2х3 + 3х + 1)' = 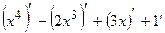 =
= 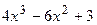 .
.
2. 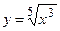
Решение. Поскольку 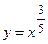 , то
, то 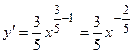 =
= 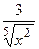 .
.
3. 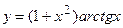
Решение. Имеем произведение функций, поэтому 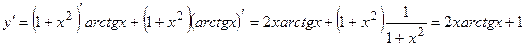
4. 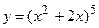
Решение. Данная функций является сложной: у = f(u), u = u(x), где u = х2 + 2х..
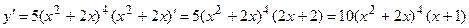
 2015-10-22
2015-10-22 350
350








