Вектор. Линейные операции над векторами

Раздел 2. ВЕКТОРНАЯ АЛГЕБРА

Студент должен:

знать:

- определение вектора, операции над векторами и их свойства, координаты вектора;

- скалярное, векторное и смешанное произведения векторов;

уметь:

- находить координаты вектора, модуль вектора, выполнять действия с векторами в координатной форме;

- вычислять скалярное, векторное и смешанное произведения векторов.

Уровни компетенций, которые может достигнуть студент при изучении данного раздела

Минимальная компетенция

Выполнять операции над векторами в координатной форме;

знать линейные операции над векторами;

уметь находить скалярное, векторное, смешанное произведение векторов.

Средняя компетенция

Применять теорию векторов к решению геометрических задач: нахождение площадей фигур и вычисление объемов тел.

Полная компетенция

Решать прикладные задачи, физические задачи, задачи на широкое применение векторной алгебры.

Вектор. Линейные операции над векторами

Вектором называется направленный отрезок. Если начало вектора находится в точке А, а конец –– в точке В, то вектор обозначается . Если же начало и конец вектора не указываются, то его обозначают строчной буквой латинского алфавита …. На рисунке направление вектора изображается стрелкой (рис. 1).

Рис. 1

Вектор, у которого начало и конец совпадают, называется нулевым и обозначается . Его направление является неопределённым. Другими словами, такому вектору можно приписать любое направление.

Векторы называются коллинеарными, если они параллельны одной прямой или лежат на одной прямой, и компланарными, если они параллельны одной плоскости или лежат в одной плоскости.

Два вектора называются равными, если они коллинеарные, одинаково направлены и равны по длине. На рис. 2 изображены пары равных векторов и (), и (). Из определения равенства векторов следует, что векторы можно переносить параллельно самим себе, не нарушая их равенства.

Рис. 2

Координатами вектора называются его проекции на оси координат Ox,Oy,Oz. Они обозначаются соответственно буквами x, y, z: .

Длиной или модулем вектора называется расстояние между его началом и концом. Записи | | и | | обозначают модули векторов и соответственно. Модуль равен квадратному корню из суммы квадратов соответствующих координат вектора

. (2.1)

Единичный вектор или орт – это вектор, длина которого равна единице. Находится по формуле:

. (2.2)

Направление вектора в пространстве определяется углами , которые вектор образует с осями координат (рис. 3). Косинусы этих углов называются направляющими косинусами вектора: .

Рис. 3

Если определены координаты вектора , тогда

. (2.3)

Свойства направляющих косинусов векторов:

1) ;

2) координаты любого единичного вектора совпадают с его направляющими косинусами: .

К линейным операциям над векторами относятся: умножение вектора на число и сложение векторов.

Произведением вектора и числа αназывают вектор, обозначаемый α , модуль которого равен |α|| |, а направление совпадает с направлением вектора , еслиα>0, и противоположно ему, если α<0. Имеем 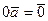для любого вектора .

Суммой векторов ( i= ) называется вектор, обозначаемый

. (2.4)

Составим из векторов–слагаемых ломаную линию, совмещая начало следующего вектора с концом предыдущего. Тогда суммой векторов будет являться вектор, начало которого находится в начале первого вектора , а конец –– в конце последнего вектора ломаной линии, составленной из последовательности слагаемых векторов (рис. 4).

Рис. 4

Это правило сложения называется правилом замыкания ломаной. В случае суммы двух неколлинеарных векторов оно равносильно правилу параллелограмма (рис. 5).

Рис. 5

Прямая l с заданным на ней направлением, принимаемым за положительное, называется осью l.

Проекцией вектора на ось l называется число, обозначаемое пр и равное (0 φ π – угол между положительным направлением оси l и направлением вектора ), т.е. по определению

пр = . (2.5)

Геометрически проекцию вектора можно охарактеризовать длиной отрезка MN, взятой со знаком “+”, если 0 φ π/2, и со знаком “–”, если π/2 φ π (рис.6). При φ=π/2 отрезок MN превращается в точку и пр =0.

Рис.6

Для равенства векторов необходимо и достаточно, чтобы их соответствующие координаты были равны. Если

M (x , y , z ) и M (x , y , z ), то

= (x –x , y –y , z –z ). (2.6)

Линейной комбинацией векторов называется вектор , определяемый по формуле

, (2.7)

где – некоторые числа. Если векторы определяются координатами x , y , z , то для координат вектора имеем:

. (2.8)

Линейные операции над векторами удовлетворяют свойствам, по форме аналогичным свойствам умножения и сложения чисел. Например,

,

,

, (2.9)

,

,

и т.д.

Если для системы n векторов равенство

= 0(2.10)

верно только в случае, когда =0 для всех значений i, то эта система называется линейно независимой.

Если же равенство (2.10) выполняется для , хотя бы одно из которых отлично от нуля, то система векторов называется линейно зависимой. Например, любые коллинеарные векторы, три компланарных вектора, четыре и более векторов в трёхмерном пространстве всегда линейно зависимы.

Три упорядоченных линейно независимых вектора , , в пространстве называются базисом. Упорядоченная тройка некомпланарных векторов всегда образует базис. Любой вектор в пространстве можно разложить по базису , , т.е. представить в виде линейной комбинации базисных векторов: в базисе , , . Базис называется ортонормированным, если его векторы взаимно перпендикулярны и имеют единичную длину. Обозначают такой базис i, j, k. В дальнейшем будем использовать только этот базис.