Пусть прямые l1 и l2 заданы уравнениями  и
и  . Угол между прямыми определяется по формуле
. Угол между прямыми определяется по формуле  .
.
Условием параллельности двух прямых является равенство их угловых коэффициентов:  .
.
Условием перпендикулярности прямых является равенство  (угловые коэффициенты обратно пропорциональны и имеют противоположные знаки).
(угловые коэффициенты обратно пропорциональны и имеют противоположные знаки).
Пусть заданы прямая 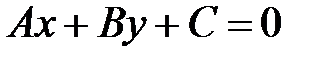 и точка М0(х0;у0). Расстояние от точки до прямой определяется по формуле
и точка М0(х0;у0). Расстояние от точки до прямой определяется по формуле  .
.
Пример 1. Найти расстояние от точки М0(2;-1) до прямой  .
.
По формуле получаем  лин. ед.
лин. ед.
Пример 2.
Даны вершины треугольника АВС: А (-2;3), В (1; 12), С (11; 6). Найти:
| Е |
| А |
| D |
| К |
| О |
| В |
| х |
| у |
| С |
| -2 |
| Рисунок 1 |
Решение. Построим треугольник в прямоугольной системе координат по заданным точкам (рис.1).
1) Уравнение прямой, проходящей через две точки А(х1;у1) и В(х2;у2) имеет вид  . Подставим в это уравнение координаты точек А (-2;3), В (1;12). Получим
. Подставим в это уравнение координаты точек А (-2;3), В (1;12). Получим  →
→  →
→  →
→  .
.
 - уравнение стороны АВ.
- уравнение стороны АВ.
2) Высота СD перпендикулярна стороне АВ. Поэтому их угловые коэффициенты связаны соотношением: kCД=-1/kАВ. Уравнение прямой АВ запишем в виде  (уравнение прямой с угловым коэффициентом k):
(уравнение прямой с угловым коэффициентом k):  . Из этого уравнения определяем угловой коэффициент прямой АВ: kАВ= 3. Тогда угловой коэффициент прямой СD: kCД= -1/3.
. Из этого уравнения определяем угловой коэффициент прямой АВ: kАВ= 3. Тогда угловой коэффициент прямой СD: kCД= -1/3.
Для составления уравнения высоты, используем уравнение прямой с угловым коэффициентом, проходящей через данную точку:  . Подставим в это уравнение координаты точки С (11; 6) и угловой коэффициент kCД. Получим искомое уравнение высоты СD.
. Подставим в это уравнение координаты точки С (11; 6) и угловой коэффициент kCД. Получим искомое уравнение высоты СD.
 →
→  →
→  - уравнение СД.
- уравнение СД.
Определим координаты точки Е, которая является серединой отрезка ВС. Координаты середины отрезка находятся по формулам:  ,
,  , где (х1;у1) и (х2;у2) –координаты отрезка.
, где (х1;у1) и (х2;у2) –координаты отрезка.
Используя координаты вершин В (1; 12) и С (11; 6), получим
 ,
,  . Координаты точки Е (6;9).
. Координаты точки Е (6;9).
Чтобы составить уравнение медианы АЕ, используем уравнение прямой, проходящей через две точки  . Подставляем координаты точек А(-2;3) и Е(6;9) в формулу, получаем:
. Подставляем координаты точек А(-2;3) и Е(6;9) в формулу, получаем:  →
→  →
→  →
→  .
.
Окончательно, уравнение медианы АЕ:  .
.
Найдем точку К пересечения прямых АЕ и СD. Для этого решим систему уравнений
 . Получим: К(62/13; 105/13).
. Получим: К(62/13; 105/13).
 2015-10-22
2015-10-22 435
435








