2015-10-22
860
- уравнение окружности с центром в точке С (α;β) радиусом R.
– каноническое уравнение эллипса.
– каноническое уравнение гиперболы.
, 
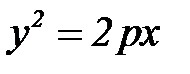– канонические уравнения параболы.
Уравнением кривой второго порядка в общем виде является выражение 
, левая часть которого есть многочлен второго порядка относительно х, у. При этом 
– квадратичная форма, 
– линейная форма, F – свободный член.
Пример 1.
Установить вид кривой второго порядка, заданной уравнением
| 4 |
| у |
| х/ |
| у/ |
| О/ |
| 3 |
| О |
| х |
| -1 |
  3 |
| Рисунок 2 |
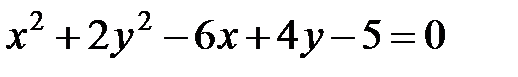. Преобразуем уравнение
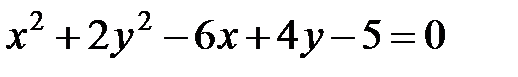, дополняя до полного квадрата слагаемые, содержащие х и у.
,
, разделим обе части уравнения на 16.
.
Обозначим 
, 
. Получим уравнение эллипса в системе координат 
, начало которой находится в точке О/(3;-1): 
.
Построим обе системы координат и эллипс. Полуоси эллипса равны 4 и 2 
(рис. 2).
Пример 2.
Составить уравнение и построить линию, каждая точка которой находится вдвое ближе к точке А(1;0), чем к точке В(-2;0).
Решение: Рассмотрим произвольную точку М(х;у), принадлежащую линии. Геометрическое свойство линии по условию задачи 
.Выразим это свойство через координаты точек А, В и М (рис. 3).
| М(х;у) |
| у |
| х |
| О |
| -2 |
| А |
| В |
| Рисунок 3 |
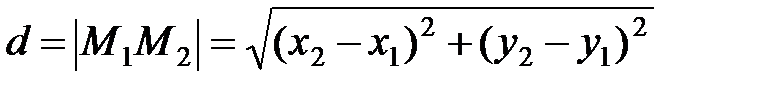. Используя эту формулу, находим: 
;
.
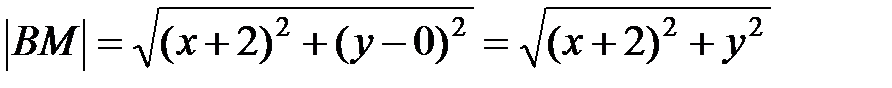Составляем уравнение для искомой линии , т.е
.
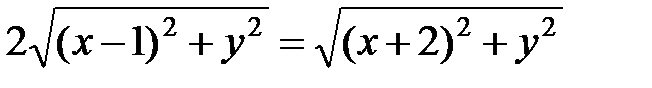Преобразуем это уравнение. Возведем обе части в квадрат, раскроем скобки, приведем подобные члены, получим:
| О |
| у |
| х |
| Рисунок 4 |
| С |
.
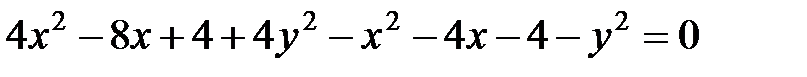
Дополним члены, содержащие х, до полного квадрата: 
; 
.
Получили уравнение окружности с центром в точке С(2; 0) и радиусом r=2.
Построим эту окружность (рис. 4).
Пример 3.
| у |
| х/ |
| у/ |
| О/ |
| 2 |
| О |
| х |
| 1 |
| Рисунок 5 |
.
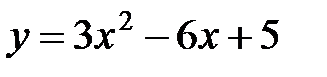Решение: Преобразуем уравнение
.
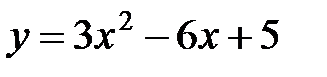
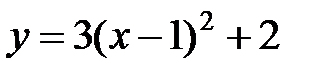
Обозначим 
, 
. Получим 
.
Это уравнение параболы в системе координат 
, начало которой находится в точке О'(1;2). Сделаем схематический чертеж (рис. 5).
