Построение эмпирических формул методом наименьших квадратов

Формулы, служащие для аналитического представления опытных данных называются эмпирическими формулами.

Аппроксимация (приближение, сглаживание) – когда по данным результатам наблюдений подбирается наиболее простая формула того или иного типа, дающая наилучшее приближение к имеющимся данным. При этом формула не воспроизводит в точности данные наблюдений.

Для получения аппроксимирующей функции чаще всего используется метод наименьших квадратов.

Пусть в результате эксперимента получено n значений функции 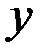при соответствующих значениях аргумента. Результаты записаны в таблицу.

			…		…
			…		…

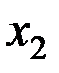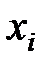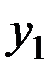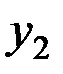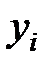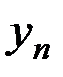Пусть зависимость между величинами х и у линейная. Требуется найти линейное уравнение .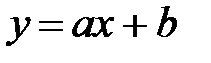

Параметры а и b находим, решая систему, которая называется нормальной:

.

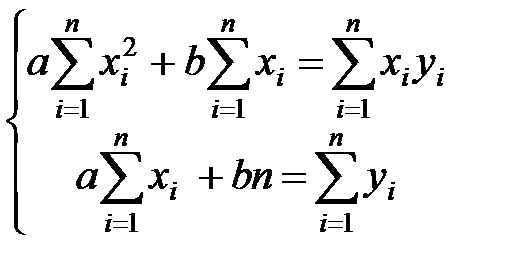Пример.

Результаты измерений представлены таблицей. Методом наименьших квадратов составить эмпирическую формулу, выражающую зависимость между х и y.

	3,5		2,5	0,5

Построить полученную прямую и экспериментальные точки.

Решение.

В прямоугольной системе координат построим данные точки. Заметим, что точки располагаются вблизи некоторой прямой, поэтому эмпирическую формулу будем искать в виде 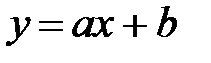. Для отыскания коэффициентов а и b составим нормальную систему. Расчеты поместим в таблицу.

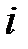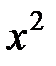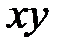		3,5		3,5	3,7
					2,94
		2,5		7,5	2,18
		0,5		2,5	0,66
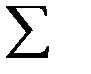		9,5		19,5

Нормальная система имеет вид:

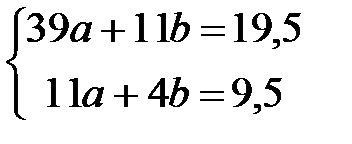
Решаем систему методом Крамера:

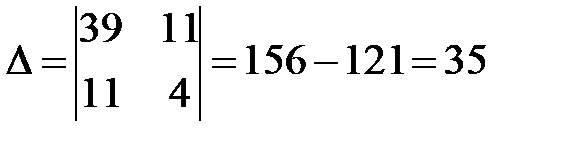
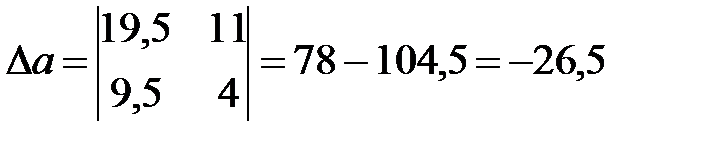
Искомая эмпирическая формула имеет вид: .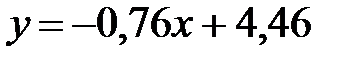

Для контроля вычислим по этой формуле значения .

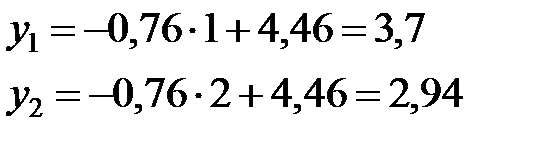
х

y

0,5

2,5

3,5

Рисунок 10

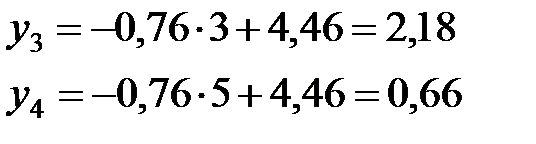
Сравнивая контрольные значения с экспериментальными данными, видим, что отклонение этих величин невелико. По любым двум значениям строим прямую. Она проходит достаточно близко к заданным точкам. Искомая прямая и экспериментальные точки изображены на рисунке 10.