Формулы Грина

Запишем формулу Остроградского-Гаусса:

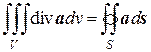. (8.32)

или, с использованием оператора Гамильтона,

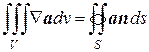. (8.33)

Иногда формулу Остроградского-Гаусса называют теоремой о дивергенции, поскольку из нее следует, что

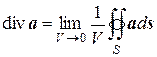. (8.34)

Используя формулы векторного анализа можно записать аналогичные выражения для ротора и градиента.

Для ротора можно записать (теорема о роторе):

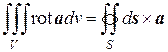. (8.35)

или, в других обозначениях,

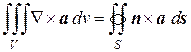. (8.36)

Правую часть в формуле (8.35) или (8.36) можно интерпретировать как векторный поток векторного поля a через поверхность S (в отличие от скалярного поля в формуле Остроградского-Гаусса). Из формулы (8.35) следует, что ротор можно определить следующим образом:

. (8.37)

Для градиента можно записать (теорема о градиенте):

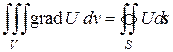, (8.38)

или, в других обозначениях,

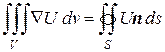. (8.39)

Правую часть в формуле (8.38) или (8.39) можно интерпретировать как векторный поток скалярного поля U через поверхность S. Из формулы (8.38) следует, что градиент можно определить следующим образом:

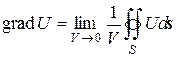. (8.40)

Отметим, что формулы (8.35) и (8.38) можно, доказать, используя теорему Остроградского-Гаусса, если применить эту формулу к каждой компоненте соответствующего векторного поля.

Замечание 1. Подобно тому, как формулы (8.35) и (8.38) были получены в результате совмещения формулы Остроградского-Гаусса с алгебраическими операциями над векторными и скалярными полями, аналогично можно получить новые формулы, используя формулу Стокса:

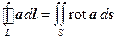. (8.41)

Эти новые формулы можно записать следующим образом:

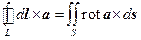, (8.42)

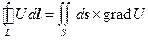. (8.43)

В теории гармонических функций заметную роль играют так называемые формулы Грина, к выводу которых мы и переходим.

Первая формула Грина имеет следующий вид

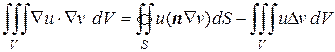. (8.44)

Действительно, поскольку

,

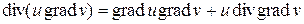то, учитывая, что div grad v =D v, получим

.

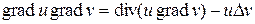Следовательно

.

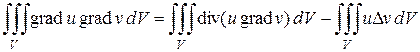Применяя к первому слагаемому правой части формулу Остроградского-Гаусса, получим

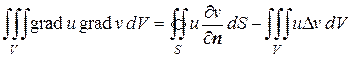. (8.45)

Перепишем формулу (8.44) следующим образом

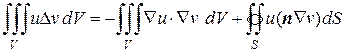. (8.46)

Меняя местами функции u и v, будем иметь

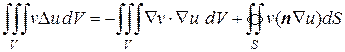. (8.47)

Вычитая из формулы (8.46) выражение (8.47), получим вторую формулу Грина:

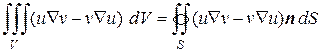. (8.48)

Из полученных формул Грина можно получить еще несколько формул. В частности, если в формуле (8.44) положить u=v, получим

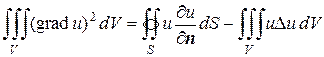; (8.49)

если в формуле (8.48) положить v º1, то получим

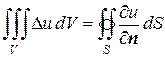. (8.50)

Равенство (8.50) иногда называют теоремой Гаусса.