Краткие сведения из теории и примеры решения задач

Пусть даны два непустых множества D и V. Если каждой паре действительных чисел (x, y) из множества D по некоторому правилу ставится в соответствие определенный элемент z из множества V, то говорят, что на множестве D задана функция. Ее обозначают .

При этом x и y называются независимыми переменными (аргументами), а z – зависимой переменной (функцией). D – область определения функции, V –множество ее значений.

Если существует конечный предел , то он называется частной производной функции по независимой переменной x. Вычисляется в предположении, что y - постоянная. Обозначается

Если существует конечный предел , то он называется частной производной функции по независимой переменной y. Вычисляется в предположении, что x - постоянная. Обозначается

Частные производные находят по формулам и правилам вычисления производных функции одной переменной.

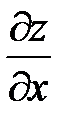Пример1. . Найти и .

Решение. Рассматривая y как постоянную, получим:

.

В предположении, что x постоянная, находим частную производную по у:

.

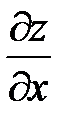Пример 2. . Найти и .

Решение.

.

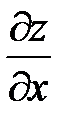Пример 3. . Найти и .

Решение.

.