Лабораторна робота № 5

Інтерполяція

Теоретичні відомості

Дана таблична функція, тобто таблиця, в якій для деяких дискретних значень аргументу x_i, розташованих в порядку зростання, задані відповідні значення функції у_i:

I	x	y=f(xi)
	x0	y0
	x1	y1
…	…	…
N	xn	yn

Точки з координатами (x_i, y_i) називаються вузловими точками або вузлами.

Припустимо, що необхідно знайти значення y_k табличної функції в будь-якій проміжній точці х_k, розташованою усередині інтервалу [x_i, x_i+1]. Для цього необхідно знайти аналітичний вигляд деякої іншої функції P(x), яка буде наближено замінювати табличну функцію f(x_i).

Задача інтерполяції полягає в тому, щоб побудувати многочлен P(x), графік якого проходить через усі вузлові точки, тобто:

,

, (5.1)

де n=N–1 ступінь многочлена; N – кількості вузлових точок.

Многочлен вигляду (5.1), який проходить через всі вузлові точки табличної функції називається інтерполяційним многочленом. Інтерполяційний многочлен можна побудувати за допомогою формули Лагранжа:

. (5.2)

Формулу можна записати у згорнутому вигляді:

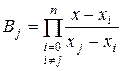, . (5.3)

Простим варіантом інтерполяції є кусково-лінійна інтерполяція. Вона полягає в простому з’єднанні між собою двох точок відрізками прямих. В цьому випадку n=1 та інтерполяційна формула має вигляд:

. (5.4)

Для реалізації такої інтерполяції в Mathcad існує вбудована функція linterp (vx,vy,x), де vx vy – вже відомі вектори, що містять координати точок; x – координата точки, в якій потрібно обчислити значення функції.

Найчастіше використовується інтерполяція, де експериментальні точки попарно з’єднуються відрізками поліномів. Якщо для цього обирають поліноми третього ступеня (кубічна парабола), то така крива називається кубічним сплайном. При цьому на кожному відрізку [x_i–1, x_i] будується многочлен третього ступеня .

У Mathcad існують три функції для побудови кубічних сплайнів, які відрізняються обмеженнями на поведінку сплайна в початковій і кінцевій експериментальних точках.

lspline (vx,vy) – в початковій і кінцевій точках накладається умова лінійності, тобто друга похідна від функції дорівнює нулю.

pspline (vx,vy) – на першому та останньому інтервалі крива є параболою, тобто поліноміальний коефіцієнт при x ³ дорівнює нулю.

cspline (vx,vy) – на перших двох і на останніх двох інтервалах поліноміальні коефіцієнти при x ³ рівні між собою.

Результатом кожної з цих функцій є вектор, що містить значення других похідних від інтерполяційної кривої в усіх точках, заданих в масиві vx.

interp (v,vx,vy,x) – повертає значення інтерполяційної функції в точках, що задані вектором x; vx і vy – масиви експериментальних точок; v – масив, отриманий як результат однієї з трьох функцій, перерахованих вище.

Сплайн-інтерполяція включає два етапи:

1. За допомогою функцій lspline, pspline або cspline отримують вектор других похідних інтерполяційної функції.

2. За допомогою функції interp обчислюються значення інтерполяційної функції в заданих точках.

Приклад 5.1. Виконати лінійну інтерполяцію та обчислити значення функції y(10,8), y(11,6), y(17,4).

X			13,5
Y		11,5			14,7		12,4

Знайдемо рівняння прямої, що з’єднує точки (10, 10) та (12, 11.5): .

Контроль значень у вузлових точках:

L(10)=7.5+2.5=10.

L(12)=0.75·12+2.5=11.5.

Обчислення наближених значень функції у проміжних точках:

L(10.8)=0.75·10.8+2.5=10.6.

L(11.6)=0.75·11.6+2.5=11.2.

Оскільки х=17,4 знаходиться на інтервалі [17, 19], то в формулу (5.4) підставимо , , , :

,

L(17.4)= –1.35·17.4+37.65=14.16.

Завдання

1. Виконати кусково-лінійну інтерполяцію за допомогою функції linterp.

2. Побудувати кубічний сплайн для табличної функції. Використовуючи знайдену залежність, знайти значення y в заданій точці х=а.

3. Побудувати інтерполяційний многочлен Лагранжа. Обчислити значення функції в заданій точці x=a.

Порядок виконання

Кусково-лінійна інтерполяція за допомогою функції linterp

N:=rows(X) N=7 – кількість рядків у заданих векторах даних

i:=0…N–1 – номер вузла

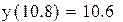
Побудова кубічного сплайну

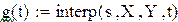
Інтерполяційний многочлен Лагранжа

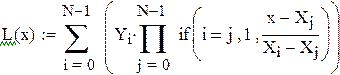
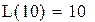
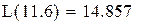
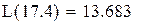
Контрольні питання

1. Постановка задачі інтерполяції.

2. Що таке глобальна та локальна інтерполяція?

3. В чому полягає кусково-лінійна інтерполяція?

4. Що таке сплайн-інтерполяція?

5. Які є функції для виконання інтерполяції в Mathcad?

Варіанти завдань

а=x₀+0.45

	Х		1.1	1.2	1.3	1.5
	Y	0.686	0.742	0.767	0.646	0.774
	Х		2.1	2.2	2.3	2.5
	Y	2.312	2.251	2.418	2.752	2.7
	Х		3.1	3.2	3.3	3.5
	Y	4.615	4.591	5.13	5.481	5.553
	Х		4.1	4.2	4.3	4.5
	Y	8.472	8.805	9.096	8.993	9.312
	Х		5.1	5.2	5.3	5.5
	Y	12.36	13.63	13.3	13.15	13.48
	Х		6.1	6.2	6.3	6.5
	Y	17.63	19.75	19.79	18.81	19.87
	Х		7.1	7.2	7.3	7.5
	Y	25.24	25.13	25.67	26.63	26.75
	Х		8.1	8.2	8.3	8.5
	Y	30.53	34.22	34.23	34.11	33.6
	Х		9.1	9.2	9.3	9.5
	Y	41.74	42.24	43.88	42.17	43.7
	Х		10.1	10.2	10.3	10.5
	Y	49.76	51.92	50.08	52.38	53.41

	Х	1.4	1.6	1.7	1.8	1.9
	Y	0.807	0.97	0.932	0.936	0.978	1.048
	Х	2.4	2.6	2.7	2.8	2.9
	Y	2.459	3.022	3.079	2.42	2.669	3.241
	Х	3.4	3.6	3.7	3.8	3.9
	Y	5.492	5.471	5.727	5.798	6.11	6.605
	Х	4.4	4.6	4.7	4.8	4.9
	Y	9.465	9.771	9.61	9.722	11.41	10.28
	Х	5.4	5.6	5.7	5.8	5.9
	Y	14.24	14.52	14.88	15.25	15.34	15.16
	Х	6.4	6.6	6.7	6.8	6.9
	Y	21.12	20.21	19.49	20.15	20.51	21.29

Продовження таблиці

	Х	7.4	7.6	7.7	7.8	7.9
	Y	27.23	26.49	26.88	27.23	28.07	27.79
	Х	8.4	8.6	8.7	8.8	8.9
	Y	34.06	34.5	35.83	35.68	35.44	35.67
	Х	9.4	9.6	9.7	9.8	9.9
	Y	45.04	42.46	45.72	44.06	45.87	44.95
	Х	10.4	10.6	10.7	10.8	10.9
	Y	54.96	52.77	54.12	55.48	55.69	56.2
	Х	1.2	1.3	1.5	1.4	1.6	1.7
	Y	0.767	0.646	0.774	0.807	0.97	0.932
	Х	2.2	2.3	2.5	2.4	2.6	2.7
	Y	2.418	2.752	2.7	2.459	3.022	3.079
	Х	3.2	3.3	3.5	3.4	3.6	3.7
	Y	5.13	5.481	5.553	5.492	5.471	5.727
	Х	4.2	4.3	4.5	4.4	4.6	4.7
	Y	9.096	8.993	9.312	9.465	9.771	9.61
	Х	5.2	5.3	5.5	5.4	5.6	5.7
	Y	13.3	13.15	13.48	14.24	14.52	14.88