ДУ первого порядка называется однородным, если его можно представить в виде 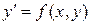 , где
, где  – однородная функция нулевой степени однородности. Однородное уравнение сводится к уравнению с разделяющимися переменными с помощью подстановки y=xt, dy=xdt+tdx.
– однородная функция нулевой степени однородности. Однородное уравнение сводится к уравнению с разделяющимися переменными с помощью подстановки y=xt, dy=xdt+tdx.
Примеры
1)  ;
;
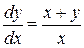
xdy=(x+y)dx, y=xt, dy=xdt+tdx
x(xdt+tdx)=(x+xt)dx
xdt+tdx=(1+t)dx
xdt+tdx=dx+tdx
xdt=dx

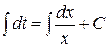
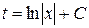 , вернемся к старой переменной
, вернемся к старой переменной
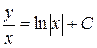
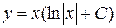 .
.
2) 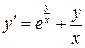
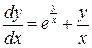
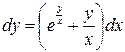
Пусть y=xt, dy=xdt+tdx,




 ;
;
- е - t =ln| x |+ C.
Вернемся к старым переменным: 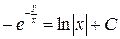 .
.
 2015-10-22
2015-10-22 329
329








