Замена переменной в определенном интеграле

Теорема. Пусть f(x) непрерывна на [ a, b ], введем подстановку . Если

1) непрерывны при ,

2) при изменении t от до , функция изменяется от a до b, , то справедлива формула замены переменной:

Пример (см. задание 2):

Вычисление площадей плоских фигур

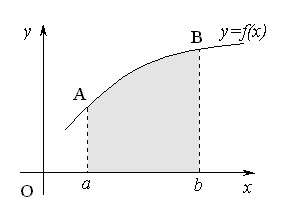
– площадь криволинейной трапеции.

Площадь фигуры, ограниченной линиями , находим по формуле

Эта формула остается справедливой при любом расположении рассматриваемой фигуры.

Пример (см. задание 3):

Вычислить площадь фигуры, ограниченной линиями: , .

1) Найдем точки пересечения данных кривых.

;

;

;

; .

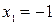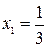2) Построим графики данных функций.

(для прямой )

(парабола ).

4 Дифференциальные уравнения

Основные понятия

1. Дифференциальным уравнением (ДУ) называется уравнение, связывающее независимую переменную, искомую функцию и ее производные:

.

2. Наивысший порядок производной искомой функции, входящей в ДУ, называется порядком ДУ.

3. Решить ДУ – это значит найти все функции, которые ему удовлетворяют, т. е. при подстановке их в уравнение, оно обращается в тождество.

4. Нахождение решений ДУ называется интегрированием ДУ, график решения ДУ называется интегральной кривой.