ДУ с разделяющимися переменными

ДУ называется уравнением с разделяющимися переменными, если его можно представить в виде ,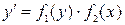

где правая часть есть произведение сомножителей, каждый из которых является функцией только одной переменной.

Способ решения: разделение переменных по соответствующим дифференциалам (при dx должна стоять функция, зависящая от x, при dy – функция зависящая от y).

Пример:

1) ;

;

;

;

;

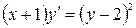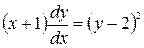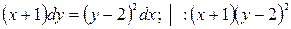
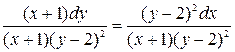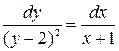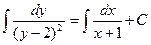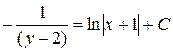– общее решение ДУ.

2) Найти частное решение уравнения 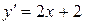, удовлетворяющее начальным условиям .

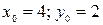Найдем общее решение

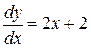
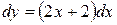
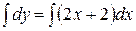
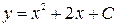– общее решение. Выделим из него частное, удовлетворяющее начальным условиям , .

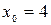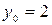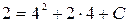; С =-22, тогда

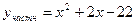– из всего семейства интегральных кривых (парабол) выделили одну, проходящую через заданную точку (4; 2).

Однородные функции

Функция f(x,y) называется однородной k -ой степени однородности, если выполняется равенство:

.

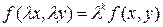В частности, если

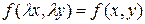– функция однородная нулевой степени однородности.

Примеры

1) .

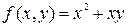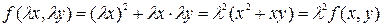– однородная функция второй степени однородности.

2) .

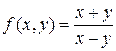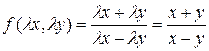– однородная функция нулевой степени однородности.