2015-10-22
755
Это уравнение вида:
 , | (3) |
где 
– многочлены степени n и m соответственно.
– Известно, что общее решение таких уравнений имеет вид
,
где 
– какое-либо частное решение неоднородного уравнения (3),
– общее решение соответствующего однородного уравнения
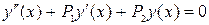
Частное решение уравнения (3) ищем в виде, подобном правой части:
 , | (4) |
где 
многочлены k -той степени с неизвестными коэффициентами, определяемыми в процессе решения, k= max{n,m}.
При этом следует составить число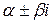 
, где 
– коэффициент при x в показателе 
, 
– коэффициент при x в аргументе синуса или косинуса (если один из них отсутствует). Если это число 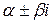не является корнем характеристического уравнения, то 
в виде (4) оставляем без изменения, если 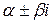есть корень кратности s (повторяется s раз), то выбранный домножаем на 
.
Примеры
1) Если 
, то смотрим является ли корнем характеристического уравнения число 
,
8 – многочлен нулевой степени, в общем виде это некоторое число, т.е. выбираем 
.
2) 
.
После предварительного выбора 
проверяем, является ли число 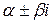корнем характеристического уравнения. Далее находим первую, вторую производную , подставляем их в первоначальное уравнение и находим A, B, C.
Примеры (см. задание 5):
а) Найдем 
, решим соответствующее однородное уравнение
, составим характеристическое уравнение
,
(корень кратности 2 – повторяется 2 раза),
тогда 
-общее решение соответствующего однородного уравнения.
б) Найдем . Его будем искать в виде, подобном правой части. Там 
-это многочлен второй степени, в общем виде это 
, т.е.
.
Число 
не является корнем характеристического уравнения, значит, оставим в выбранном виде. Теперь найдем неизвестные коэффициенты 
. Так как – есть решение первоначального дифференциального уравнения, то оно обращает это уравнение в тождество. Найдем 
и подставим в первоначальное уравнение
Два многочлена тождественно равны тогда и только тогда, когда равны их коэффициенты при одинаковых степенях неизвестного. Приравняем коэффициенты при 
(свободный член) в обеих частях
тогда
.
Общее решение
.
,
а) 
-решаем соответствующее однородное уравнение. Составим его характеристическое уравнение.
б) ,
-является корнем характеристического уравнения, тогда домножим на x, так как пара 
повторяется один раз, тогда окончательно
.
Найдем A и B.
Подставим в первоначальное ДУ
Приравниваем коэффициенты при sin x и cos x
,
тогда 
.
Замечание. Если в правой части отсутствуют 
и 
, частное решение ищем все равно в виде суммы двух слагаемых.
