Коэффициентами
Это уравнения вида
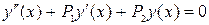 , ,
| (1) |
где 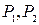 – константы.
– константы.
Общее решение такого уравнения имеет вид
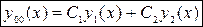
где 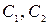 – произвольные постоянные
– произвольные постоянные
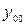 -общее решение однородного уравнения,
-общее решение однородного уравнения,
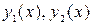 -линейно независимые частные решения уравнения (1).
-линейно независимые частные решения уравнения (1).
Определение. Функции 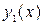 и
и 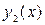 называются линейно независимыми (зависимыми) на (a, b), если при
называются линейно независимыми (зависимыми) на (a, b), если при 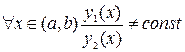
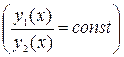
Решение уравнения (1) сводится к решению алгебраического уравнения
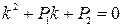 , ,
| (2) |
называемого характеристическим, в котором степень k равна порядку производной в уравнении (1).
При этом возможны следующие случаи:
1. При 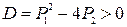 уравнение (2) имеет действительные различные корни
уравнение (2) имеет действительные различные корни 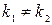 , тогда частные решения ДУ (1) имеют вид
, тогда частные решения ДУ (1) имеют вид 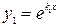 ,
,  (в чем можно убедится непосредственной подстановкой).
(в чем можно убедится непосредственной подстановкой).
Они линейно независимы (смотри определение). Тогда общее решение (1) имеет вид:
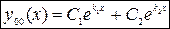
2. При 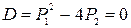 характеристическое уравнение (2) имеет два действительных равных корня
характеристическое уравнение (2) имеет два действительных равных корня 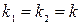 , тогда частными решениями Д.У. (1) являются функции
, тогда частными решениями Д.У. (1) являются функции 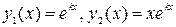 , общее решение (1) имеет вид
, общее решение (1) имеет вид
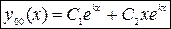
3. Если  , то характеристическое уравнение (2) не имеет действительных корней, но имеет комплексные корни вида
, то характеристическое уравнение (2) не имеет действительных корней, но имеет комплексные корни вида 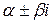 .
.
Тогда частные решения 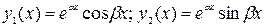
Общее решение (1) имеет вид
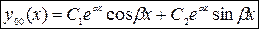
Примеры (см. задание 5):
1) 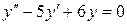 , составим характеристическое уравнение:
, составим характеристическое уравнение: 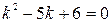
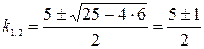 ;
; 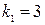 ;
; 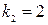 .
.
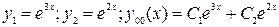
2) 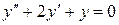 , составим характеристическое уравнение
, составим характеристическое уравнение 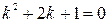
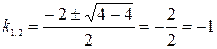 ;
;
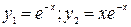 ;
;
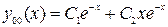 .
.
3) 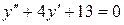
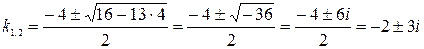
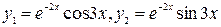
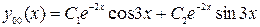
4) 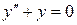
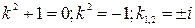
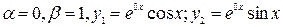
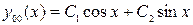
 2015-10-22
2015-10-22 603
603








