Пусть на некоторую стержневую систему действует произвольная нагрузка. Внутренние силы, соответствующие этому состоянию обозначим индексом “ F ”. Таким образом, на элемент конструкции длиной ds в этом состоянии действуют внутренние силы 
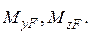

Пусть требуется определить перемещение точки i в заданном направлении. Приложим в этом направлении единичную силу Fi =1. Внутренние усилия, соответствующие этому состоянию, обозначим индексом ‘ i ’ и чертой сверху. Таким образом, внутренние силы i -ого единичного состояния есть 

,
Применим принцип возможных перемещений: если механическая система находится в равновесии, то суммарная работа внешних и внутренних сил на любых возможных бесконечно малых перемещениях, не противоречащих кинематическим связям системы, равна нулю.
При этом в качестве возможного будем рассматривать заданное состояние, а в качестве действительного - единичное состояние.
Математическая запись принципа возможных перемещений имеет вид:
 | (6.1) |
В уравнении (6.1) АiF – работа внешних сил единичного состояния на перемещениях грузового, ViF - работа внутренних сил единичного состояния на перемещениях грузового.
Работа внешних сил находится так:
 | (6.2) |
т.к. 
Работу внутренних сил единичного состояния на перемещениях грузового найдем сначала в пределах элемента ds, причем сделаем это отдельно для каждой составляющей внутренних сил.
Растяжение-сжатие

Удлинение элемента ds в грузовом состоянии равно
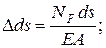
Работа внутренней продольной силы единичного состояния на этом перемещении равна
 | (6.3) |
Кручение

Угол закручивания элемента ds в грузовом состоянии равен

Работа внутреннего крутящего момента единичного состояния на этом перемещении равна
 | (6.4) |
 2015-10-22
2015-10-22 1551
1551
