Определение усилий в стержнях ферм

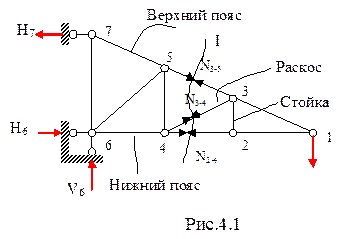
Фермами называются конструкции, составленные из стержней, соединенных между собой при помощи шарниров. Стержни, образующие внешний контур ферм, называют обычно поясами, остальные стержни – решеткой. Решетки состоят из раскосов (наклонных элементов) и стоек (вертикальных элементов). Расстояние между двумя соседними узлами пояса называют панелью (рис. 4.1).

В стержнях ферм возникают только продольные усилия. В статически определимых фермах эти усилия могут быть найдены с помощью уравнений равновесия. Для кинематического анализа ферм можно пользоваться общими формулами, приведенными в лекции 1, но можно получить и более простые. При этом будем считать основными элементами ферм их узлы, а стержни будем рассматривать как кинематические связи.

Тогда число степеней свободы фермы будет выражаться формулой:

(4.1)

где y – число узлов, С ₀ – число опорных стержней, С – число внутренних стержней.

Для фермы, изображенной на рис. 4.1 имеем: y = 7; С ₀ = 3; С = 11, следовательно, n = 2 * 7 - 11 - 3 = 0 и ферма статически определима. Она геометрически неизменяема, поскольку состоит из простейших шарнирных треугольников.

Для определения усилий в стержнях ферм используется способ сечений. Рассмотрим различные модификации этого способа.

Способ вырезания узлов

При реализации этого способа последовательно вырезаются узлы фермы и для каждого из них составляются уравнения равновесия в виде суммы проекций всех внешних и внутренних сил, действующих на данный узел, на две не параллельные друг другу оси. В общем случае получается система из 2y уравнений равновесия, из которых и могут быть найдены С+С ₀ усилий как в стержнях фермы, так и в опорных стержнях.

Всегда, однако, можно выбрать такую последовательность вырезания узлов, при которой каждый раз нужно будет решать не более двух уравнений с двумя неизвестными. Начинать нужно с того узла, в котором сходится не более двух стержней с неизвестными усилиями. Например, при расчете фермы рис. 4.1 необходимо начать с узла 1, в котором сходится два стержня. Вырежем этот узел (рис.4.2) и составим для него уравнения равновесия.

Усилия в стержнях можно обозначать по-разному. Рекомендуем обозначать их буквой N с индексами, показывающими, к каким узлам прикреплен данный стержень. При этом неизвестное усилие рекомендуется считать растягивающим. Знак минус у результата будет означать, что стержень на самом деле сжат.

В рассматриваемом примере N_1-3 можно сразу найти из уравнения проекции на ось Y:

Усилие N_1-2 можно найти теперь из уравнения проекций на ось X:

Вырежем узел 2 (рис. 4.3). Из уравнения проекций на ось Y находим:

Из уравнения проекций на ось X получаем:

Действуя аналогичным образом, можно найти усилия во всех стержнях, в том числе и опорных. Заметим, что, если бы мы попытались после первого узла сразу перейти к третьему, то получили бы для этого узла два уравнения с тремя неизвестными Заметим также, что усилия в стержне 2-3 равны нулю, и возникает вопрос о целесообразности использования этого стержня в данной конструкции. В общем случае включение подобных стержней в состав конструкции объясняется конструктивными соображениями, например, стремлением собрать конструкцию из более коротких стержней, которые, к тому же, оказываются и более устойчивыми.

При расчете способом вырезания узлов ферм на двух опорах (см. рис. 4.4), необходимо в первую очередь найти опорные реакции.

Отметим, что при определении усилий в стержнях статически определимых ферм полезно помнить приведенные ниже правила, не требующие доказательств (леммы).

Лемма 1. Если в конструкции фермы имеется трехстержневой узел, в котором два стержня лежат на одной прямой, а третий, называемый одиночным, - под углом к ним, и если в узле приложена внешняя сила, направленная вдоль одиночного стержня, то усилия в первых двух стержнях равны между собой, а усилие в одиночном стержне равно внешней силе.

Лемма 2. Если в ненагруженном трехстержневом узле фермы имеется одиночный стержень, то усилие в этом стержне равно нулю.

Способ разрезов

При использовании этого способа ферма мысленно рассекается на две части, одна часть отбрасывается, действие ее заменяется силами, и для оставшейся части составляются три уравнения равновесия. Разрез нужно проводить так, чтобы в него попало не более трех стержней с неизвестными усилиями. Уравнения равновесия целесообразно составлять таким образом, чтобы они решались независимо друг от друга.

Это всегда можно сделать, если придерживаться приведенного выше правила разрезания фермы. Так, если три стержня, попавшие в разрез, не параллельны друг другу, то для определения усилий в одном из них можно составить уравнения равновесия в виде суммы моментов всех сил, действующих на отсеченную часть, относительно точки пересечения двух других стержней. Эта точка называется моментной точкой, а сам способ составления уравнений равновесия – способом моментной точки.

Если два стержня из трех, попавших в разрез, параллельны между собой, а третий расположен под углом к ним, то для определения усилия в наклонном стержне уравнения равновесия следует составлять в виде равенства нулю сумм проекций всех сил, действующих на отсеченную часть фермы, на направление, перпендикулярное двум параллельным стержням. Такой способ составления уравнений равновесия называется способом проекций.

Проиллюстрируем сказанное примерами.

Пример 1.

Найдем усилия в стержнях второй панели слева фермы, изображенной на рис.4.4. Проведем сечение I (попытки проведения сечения II или сечения III, как показано на рис. 4.4 пунктиром, следует признать неудачными, т.к. они проходят через четыре стержня с неизвестными усилиями). Для определения усилия N _3-5 выберем моментную точку в узле 2 и составим для левой отсеченной части уравнения моментов относительно этой точки.

Получим:

Для определения усилия в стержне 2-5 составим уравнения равновесия любой отсеченной части в виде суммы проекций всех сил на вертикальную ось:

Пример 2.

Для фермы, изображенной на рис.4.5, найдем усилия в стержнях второй панели слева, включая обе стойки, при следующих данных: d = 3 м, h = 4 м, Р = 4 кН.

	I

 

5

Решение.

1. Определение опорных реакций

Ввиду симметрии схемы конструкции и приложенной нагрузки опорные реакции в данном случае равны между собой, т.е

2. Определение внутренних усилий

Усилия в стойках находим на основании леммы 1.

Получаем:

Усилие в стержне А-3 находим методом моментной точки. В качестве моментной точки принимаем точку пересечения стержней 1-2 и А-2. Проводим сечение I и составляем уравнение равновесия левой отсеченной части фермы в виде суммы моментов всех сил относительно точки 2:

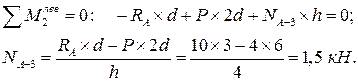
Усилие в стержне 1-2 также найдем методом моментной точки. В качестве моментной точки выберем узел А. Получим:

Чтобы воспользоваться полученным уравнением, необходимо найти плечо усилия , т.е. длину перпендикуляра , опущенного из моментной точки А на направление усилия . Эта задача решается геометрическим путем. Очевидно, что

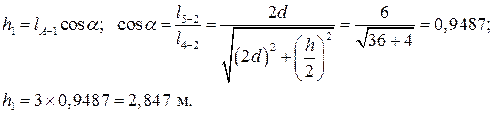
Подставляя значение в уравнение равновесия, находим

Усилие в стержне А-2 находим методом проекций:

Отсюда

Значение находим из прямоугольного треугольника А-3-2 а значение - из треугольника 4-4'-2:

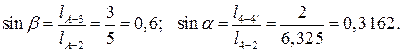
Окончательно получаем:

Таким образом, определение усилий в стержнях статически определимых ферм не представляет больших трудностей. В данной лекции описаны два метода: метод вырезания узлов и метод разрезов, хотя, по сути дела, речь идет о модификациях одного и того же универсального метода – метода сечений. Разделяя способы, автор следуют здесь традиции, установившейся в строительной механике стержневых систем.