Формула полной вероятности. Формула Байеса

Формула полной вероятности

Рассмотрим события , удовлетворяющие условиям:

1. События попарно независимы.

2. События образуют полную группу событий, то есть .

3. В результате опыта обязательно произойдет одно из этих событий.

События , удовлетворяющие перечисленным выше условиям, называют гипотезами.

Теорема. Вероятность появления события , которое может наступить лишь при условии появления одного из несовместных событий , образующих полную группу, равна сумме произведений вероятностей этих событий на соответствующие условные вероятности события .

–

формула полной вероятности.

Формула Байеса

Пусть событие произошло, и мы хотим переоценить вероятность гипотез, которые нам были известны до опыта, то есть найти условную вероятность после того, как событие произошло.

Теорема (Формула Байеса). Пусть - полная группа событий и – некоторое событие положительной вероятности. Тогда условная вероятность того, что произошло событие , если в результате эксперимента наблюдалось событие , может быть вычислена по формуле:

– формула Байеса.

Пример. Есть 3 завода, производящих одну и ту же продукцию. При этом 1-й завод производит 25%, 2-й завод — 35% и 3-й завод — 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции 3-го завода. Вся продукция смешивается и поступает в продажу. Найти:

а) вероятность купить бракованное изделие;

б) вероятность того, что купленное изделие изготовлено 2-м заводом, если это изделие бракованное.

Решение. Изделие выбирается наудачу из всей произведенной продукции. Рассмотрим три гипотезы: = {изделие изготовлено -м заводом}, .. Вероятности этих событий даны:

= 0,25,

= 0,35,

= 0,4.

Пусть событие = {изделие оказалось бракованным}. Даны также условные вероятности:

= 0,05,

= 0,03,

= 0,04.

Тогда:

а) вероятность равна доле бракованных изделий в объеме всей продукции, то есть по формуле полной вероятности

б) вероятность равна доле брака 2-го завода среди всего брака, то есть по формуле Байеса:

Пример. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0,001. Можно сделать два предположения об эксперименте:

= {стреляет 1-й стрелок}

= {стреляет 2-й стрелок}.

Априорные (a’priori —«до опыта») вероятности этих гипотез одинаковы: .

Рассмотрим событие A = {пуля попала в мишень}. Известно, что

=0,5, = 0,001.

Поэтому вероятность пуле попасть в мишень .

Предположим, что событие A произошло. Какова теперь апостериорная (a’posteriori — «после опыта») вероятность каждой из гипотез ? Очевидно, что первая из этих гипотез много вероятнее второй (а именно, в 1000 раз). Действительно,

,

.

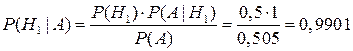Пример. Два охотника одновременно стреляют в цель. Известно, что вероятность попадания у первого охотника равна 0,2, у второго – 0,6. В результате первого залпа оказалось одно попадание в цель. Какова вероятность того, что промахнулся первый охотник?

Решение. Событие {одно попадание в цель}.

В условиях данной задачи можно сделать следующие предположения (гипотезы):

{попали в цель оба охотника}, = ;

{попал в цель первый охотник, а второй промахнулся}, ;

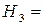{попал в цель второй охотник, а первый промахнулся}, ;

{оба охотника промахнулись}, .

Условные вероятности события при условии осуществления каждой из гипотез:

,

,

,

.

Вероятность одного попадания в цель найдем по формуле полной вероятности:

.

Найдем теперь вероятность того, что промахнулся первый охотник, то есть требуется переоценить вероятность 3-ей гипотезы, если известно, что произошло одно попадание:

.

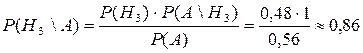Схема Бернулли

Формула Бернулли

Пусть проводиться серия испытаний, причем вероятность события в каждом испытании не зависит от исходов других испытаний. Такие испытания называют независимыми относительно события .

Событие в различных испытаниях может иметь либо различные вероятности, либо одну и ту же. Будем рассматривать такие испытания, в которых событие имеет одну и ту же вероятность.

Схемой Бернулли называется последовательность независимых испытаний, в каждом из которых возможны лишь два исхода — «успех» (событие произошло) и «неудача» (событие не произошло), при этом «успех» в одном испытании происходит с вероятностью , «неудача» — с вероятностью .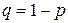

Вероятность того, что событие произойдет ровно раз из испытаний, причем не важно, в какой последовательности появиться событие , будет равна:

– формула Бернулли.

Число успехов , которому при заданном соответствует максимальная биномиальная вероятность , называется наиболее вероятным (наивероятнейшим) числом успехов.

В испытаниях схемы Бернулли с вероятностью успеха наиболее вероятным числом успехов является

- единственное число , если число не целое;

- два числа и , если число целое.

удобно искать из системы неравенств: .

Пример. Баскетболист забрасывает мяч в корзину с вероятностью 0,6. Произведено 8 бросков. Найти вероятность того, что при этом будет ровно 2 попадания. Найти наивероятнейшее число попаданий и вероятность этого числа попаданий.

Решение. Проводится серия из восьми испытаний с двумя исходами в каждом: попадание («успех») и промах («неудача»). Вероятность «успеха» при каждом испытании одна и та же: 0,6. Будем считать испытания независимыми. Требуется найти вероятность события ={в серии из 8 испытаний «успех» произошёл 2 раза}. Имеем: , , .

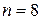По формуле Бернулли: .

Найдём наивероятнейшее число попаданий и соответствующую вероятность. Составляем систему неравенств:

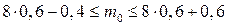, , тогда .

Соответствующая вероятность:

Итак, вероятнее всего из 8 бросков баскетболист попадёт 5 раз, причём вероятность этого события равна 0,28.