Формулировка задачи оптимального управления электропривода

Для отыскания наилучшего управления необходимо предварительно выбрать определённую оценку эффективности работы электропривода и выяснить, какие условия ограничивают характер протекания переходных процессов электроприводе.

Можно выделить две основные группы электроприводов.

Электроприводы первой группы обеспечивают перемещение исполнительного механизма; к ним относятся транспортные установки, подъемники и лифты, вспомогательные механизмы прокатных станов и много других приводов. Мерой эффективности работы электроприводов первой группы служит величина интеграла (9.74).

Ко второй группе относятся электроприводы, осуществляющие изменение скорости исполнительного механизма, например стартеры, разгонные электродвигатели газовых турбин и т.д. Мерой эффективности электроприводов второй группы является величина изменения скорости за время Т или, в интегральной форме, величина интеграла:

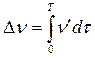. (9.78)

Поскольку электроприводы первой группы имеют значительно более широкое распространение, чем электроприводы второй группы, под словом электропривод будет подразумеваться электропривод первой группы.

Рассмотрим ограничения, накладываемые на ток якоря и скорость вращения электродвигателя. Условия механической прочности, а также насыщение питающего генератора накладывают ограничение на максимальную скорость вращения. Она не должна превышать некоторую, предельно допустимую величину:

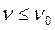. (9.79)

Условия коммутации на коллекторе накладывают ограничения на величину тока якоря. Вообще говоря, поскольку условия коммутации зависят от скорости вращения, должно выполняться неравенство:

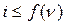. (9.80)

Ограничение (9.80) часто записывают в упрощенном виде, не учитывая зависимости условий коммутации от скорости.

Тогда ограниченным оказывается модуль тока якоря

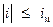. (9.81)

Весьма существенным является ограничение по нагреву, по предельно допустимой температуре изоляции обмоток.

Температура изоляции определяется потерями в двигателе и его теплоотдачей. Из потерь двигателя будем пока учитывать только потери в меди якоря. Теплоотдачу двигателя примем не зависящей от скорости и будем учитывать её по методу средних потерь. При таких допущениях ограничение по нагреву сводится к выполнению неравенства

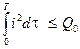, (9.82)

где 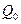− предельно допустимое количества тепла, которое может выделиться в обмотке якоря за время Т, не приводя ещё к перегреву изоляции.

Значение Q ₀ определяется условиями работы электропривода. В режиме непрерывной работы Q ₀ = T. Если работа двигателя перемежается паузами, то Q ₀ > T и зависит от того, насколько двигатель успевает охладиться за время пауз. Методы определения Q ₀ изложены в руководствах по электроприводу.

В уравнении (9.77) момент сопротивления μ − заданная функция, а током якоря и скоростью вращения мы можем управлять, регулируя, например, напряжение на зажимах двигателя. Естественно, что возникает задача оптимального управления, при котором достигаются наивысшие показатели работы электропривода при выполнении неравенств (9.79)…(9.82).

В зависимости от требований технологического процесса задача оптимального управления может формулироваться по-разному. Так, для электроприводов первой группы возможны следующие формулировки:

1. Оптимальное управление должно обеспечивать максимально возможное перемещение исполнительного механизма за время Т при заданном уровне потерь в якоре и выполнении обусловленных требованиями технологического процесса неравенств (9.79)…(9.81).

2. Оптимальное управление должно обеспечивать минимально возможные потери в якоре при выполнении заданного перемещения исполнительного механизма за время Т и соблюдении неравенств (9.79)…(9.81).

3. Оптимальное управление должно обеспечивать выполнение заданного перемещения за наименьшее время при заданном уровне потерь в якоре и выполнении неравенств (9.79)…(9.81).Такое управление часто называют оптимальным по быстродействию.

Для электроприводов второй группы достаточно в приведённых выше формулировках заменить «перемещение» на «изменение скорости».

Необходимо отметить, что все три формулировки тождественны, т.е. закон управления, отвечающий первой формулировке задачи оптимального управления, отвечает также второй и третьей формулировкам. Поэтому при решении задачи оптимального управления можно исходить из любой её формулировки. Обычно самой удобной является первая.

Под решением задачи оптимального управления будем подразумевать отыскание функций i (τ) и v (τ), обеспечивающих наилучшие показатели работы электропривода. Учитывая сказанное выше относительно тождественности различных формулировок, задачу оптимального управления о наилучших диаграммах тока и скорости для электроприводов первой группы можно математически сформулировать так:

Найти функции i (t) и n(t), связанные между собой уравнением (9.75) и доставляющие минимум интегралу (9.77) при заданном значении интеграла (9.76) и граничных условиях n(0) = n₁; n (Т) = n₂ (формулировка о минимуме потерь).

Другая формулировка задачи: найти диаграммы тока и скорости, т. е. функции i (t) и n(t), обеспечивающие наименьшее время перемещения ковша, т. е. минимум интеграла

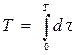(9.83)

при заданных значениях интегралов (9.76) и (9.77), граничных условиях n(0) = n₁; n (Т) = n₂ и уравнении связи (9.74) (формулировка о наивысшем быстродействии).

Наконец, возможна еще и третья формулировка задачи об оптимальных диаграммах:

найти функции i (t) и n(t), доставляющие (при тех же граничных условиях и уравнении связи) максимум интегралу (9.76) при заданном значении интеграла (9.77), т. е. максимальное перемещение при заданном уровне потерь в якоре (формулировка о максимальной производительности).

Таким образом, проблема отыскания оптимального управления электроприводом сводится к решению общей задачи Лагранжа вариационного исчисления, осложненной тем, что из-за наличия неравенств (9.79)…(9.81) часто оказывается возможной только односторонняя вариация.

В обычных задачах вариационного исчисления, где ограничения в виде неравенств отсутствуют, искомая функция, доставляющая экстремум, должна удовлетворять уравнению Эйлера, которое позволяет нам фактически определить искомую функцию — экстремаль. В отличие от этого в задачах с односторонней вариацией могут встретиться три различные возможности. Неравенства (9.79)…(9.81), а также и другие неравенства, обусловленные требованиями технологического процесса различных производственных механизмов, ограничивают некоторую область, внутри которой только и могут находиться разыскиваемые нами функции i (t) и n(t). В зависимости от того, каким образом расположены решения уравнения Эйлера — экстремали — относительно допустимой области изменения переменных i и n, могут встретиться следующие возможности:

1. Экстремали целиком находятся внутри допустимой области. В этом случае решение задачи оптимального управления определяется обычными методами вариационного исчисления и наличие неравенств (9.79)…(9.81) на решение не влияет.

2. Экстремали целиком проходят вне допустимой области. В этом случае оптимальным управлением является управление, проходящее по границе допустимой области, т. е. искомые функции i (t) и n(t) в данном случае — граничные кривые.

3. Экстремали пересекают границы допустимой области. В этом случае решение «склеено» из кусков экстремалей и кусков граничных кривых.

Таким образом, решение задачи оптимального управления следует начинать с нахождения экстремалей, т. е. решать задачу без учета ограничений (9.79)…(9.81). После этого нужно исследовать, не уходят ли экстремали за пределы допустимой области.

Определение оптимальных диаграмм тока и скорости актуально не только для экскаваторов, но и для многих других электроприводов. Главные электродвигатели реверсивных прокатных станов, электропривод манипуляторов, толкателей, и других вспомогательных механизмов прокатного производства, т. е. все электроприводы, осуществляющие циклические перемещения исполнительных механизмов, достигают своей наивысшей производительности или быстродействия при оптимальных диаграммах тока и скорости.