| № последней цифры зачетной книжки | |||||||||
| Номера задач | |||||||||
Механика
Глава 1. Кинематика материальной точки
Контрольные вопросы
1. Что изучает физика?
2. Как строится система единиц? Назовите основные и дополнительные физические величины СИ и единицы их измерения.
3. Назовите дольные и кратные приставки в СИ от 10-12 до 1012.
4. Какими свойствами обладают пространство и время в механике Ньютона?
5. Перечислите основные понятия кинематики и поясните их.
6. Что означает задать движение? Какие способы задания движения Вы знаете? Поясните их суть.
7. Что такое скорость и ускорение? Как найти величину скорости и ускорения?
8. Какие движения означают равенства: v = const и 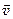 = const?
= const?
9. Что Вы можете сказать о движениях при которых a = const и 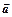 = const?
= const?
10. Охарактеризуйте ускорение при криволинейном движении. Начертите треугольник ускорений для a т < 0.
11. Вспомните определения угловых характеристик движения и направления векторов 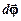 ,
, 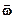 ,
, 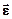 .
.
12. Установите связи между линейными и угловыми характеристиками движения.
13. Запишите законы перемещения и скорости в векторной форме и в проекциях на оси координат.
14. Установите связь между формулами пути и скорости, с одной стороны, и углового перемещения и угловой скорости – с другой.
Основные формулы
Скорость 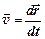 ,
,
где 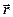 - радиус вектор точки;
- радиус вектор точки;
ускорение 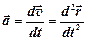 .
.
При равнопеременном движении (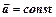 ) скорость и перемещение выражаются соотношениями
) скорость и перемещение выражаются соотношениями
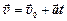 (*),
(*), 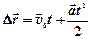 (**),
(**),
где 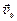 - начальная скорость.
- начальная скорость.
Формулы (*) и (**) дают возможность графически решать задачи на нахождение 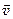 и
и 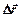 .
.
Основным методом решения задач в физике является аналитический (численный) метод. Для этого уравнения (*) и (**) проектируют на выбранные оси координат (оси движений), после чего решают полученные скалярные уравнения. В проекциях эти уравнения выглядят так
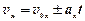 ,
, 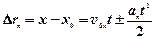 (***)
(***)
(аналогично на оси 0Y и 0Z).
Если движение происходит в одном направлении, то (***) дает пройденный путь
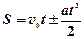 .
.
В случае равномерного (а = 0) движения
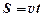 .
.
Средняя скорость
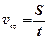 .
.
В случае равнопеременного движения в одном направлении
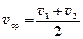 ,
,
где 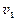 ,
, 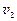 - скорости точки в моменты времени
- скорости точки в моменты времени 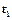 и
и 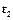 .
.
Скорость сложного движения
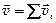 ,
,
где 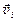 - скорости простых движений.
- скорости простых движений.
Аналогично для ускорений
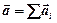 .
.
При криволинейном движении полное ускорение
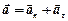 ,
,
где 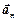 - нормальное ускорение,
- нормальное ускорение, 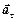 - тангенциальное (касательное) ускорение.
- тангенциальное (касательное) ускорение.
Модуль полного ускорения
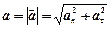 ,
,
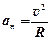 ,
, 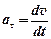 ,
,
где R - радиус кривизны траектории в данной точке.
При вращении твердого тела около неподвижной оси (или движения точки по окружности) угловая скорость
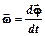 ,
,
угловое ускорение
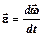 .
.
При равнопеременном вращении (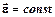 )
)
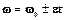 ,
,
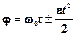 .
.
(знак “ - “ у e соответствует равнозамедленному вращению).
Связь линейных и угловых характеристик движения:
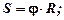
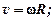
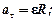
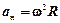
 .
.
Если 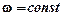 (равномерное вращение), то
(равномерное вращение), то 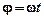 ;
;
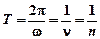 ,
,
где Т - период вращения; n - число оборотов в с; n - частота вращения.
Полезно помнить следующие два соотношения для равнопеременных движений
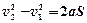 ;
; 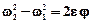 .
.
 2015-10-22
2015-10-22 902
902








