| Приклад 1.Два паралельні нескінченно довгі провідники, по яких течуть в одному напрямку електричні струми силою 60 А, розташовані на відстані 10 см один від одного. Визначити магнітну індукцію поля, створеного провідниками зі струмом у точці А, що знаходяться від одного проводу на відстані 5 см, а від іншого – 12 см (рис. 4.1). |  Рис. 4.1. Рис. 4.1. |
Дано: I =60A, d =0.1 м, r 1 =5?10–2 м, r 2 = 12?10–2 м.
Знайти: B.
Розв’язок.  Відповідно до принципу суперпозиції магнітна індукція
Відповідно до принципу суперпозиції магнітна індукція  в шуканій точці визначається як векторна сума магнітних індукцій
в шуканій точці визначається як векторна сума магнітних індукцій  і
і  полів, створених кожним провідником окремо.
полів, створених кожним провідником окремо.  . Модуль вектора
. Модуль вектора  може бути знайдений з теореми косинусів
може бути знайдений з теореми косинусів


 .
.

 У свою чергу В 1 і В 2 визначаються формулами
У свою чергу В 1 і В 2 визначаються формулами
 ;
;  .
.
Після підстановки цих виразів знайдемо
 .
.
Обчислимо 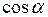 з трикутника АСD, де кут
з трикутника АСD, де кут  DAC =
DAC =  (як кути, утворені взаємно перпендикулярними сторонами)
(як кути, утворені взаємно перпендикулярними сторонами)
 .
.
Звідси
 .
.
Обчислення.
 Тл.
Тл.
Відповідь: B = 3,08·10-4 Тл.
| Приклад 2. Ізольований прямолінійний провідник зігнутий під прямим кутом із стороною, довжина якої 20 см. У площині кута поміщений кільцевий провідник радіусом 10 см так, що сторони кута є дотичними до кільцевого (рис. 4.2 а). Знайти індукцію у центрі кільця. Сили струмів у провідниках дорівнюють 2 А. |  Рис. 4.2. Рис. 4.2. |
Дано: l = 0,2 м, r 0 = 0,1 м;  ; I 1 = I 2 = I = 2 A.
; I 1 = I 2 = I = 2 A.
Знайти: В.
Розв’язок. Магнітна індукція поля в точці М відповідно до принципу суперпозиції визначається векторною сумою магнітних індукцій полів кільцевого і прямолінійного провідників зі струмом. Індукція в центрі кільцевого провідника  .
.
Індукція, створена в точці М відрізком АВ прямого провідника на відстані r 0 від нього дорівнює (рис. 4.2 б):  .
.
Цю формулу в деяких випадках зручно записувати у виді
 .
.
За умовою задачі  індукція від двох сторін кута складає
індукція від двох сторін кута складає
 .
.
Правило правого гвинта дозволяє встановити, що напрямок векторів індукцій полів В 1 і В 3, створених провідниками, збігаються, тому результуюча індукція в центрі кільця дорівнює їх алгебраїчній сумі
 .
.
Обчислення.
 Тл.
Тл.
Відповідь: B = 15,32·10-4 Тл.
Приклад 3. Протон, що пройшов прискорюючу різницю потенціалів 600 В, влетів в однорідне магнітне поле з індукцією 0,3 Тл і почав рухатися по колу. Обчислити радіус кола.
Дано: U = 600 B; B = 0,3 Тл;  = 900; m = 1,67?10–27 кг.
= 900; m = 1,67?10–27 кг.
Знайти: R.
Розв’язок. У магнітному полі з індукцією  на заряд, що рухається, діє сила Лоренца
на заряд, що рухається, діє сила Лоренца 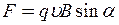 . Рух заряду буде відбуватися по колу тільки в тому випадку, коли частинка влітає у магнітне поле перпендикулярно лініям магнітної індукції
. Рух заряду буде відбуватися по колу тільки в тому випадку, коли частинка влітає у магнітне поле перпендикулярно лініям магнітної індукції  , тобто
, тобто  . Тоді
. Тоді  . Ця сила перпендикулярна векторові швидкості і надає частинці доцентрове прискорення
. Ця сила перпендикулярна векторові швидкості і надає частинці доцентрове прискорення 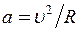 .
.
Відповідно до другого закону Ньютона можна записати 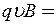
 , звідки
, звідки  . Кінетичну енергію
. Кінетичну енергію  протон набуває за рахунок роботи сил електричного поля
протон набуває за рахунок роботи сил електричного поля  , тому
, тому 
 і
і  . Підставляючи знайдену швидкість
. Підставляючи знайдену швидкість  у вираз для радіуса R, одержимо
у вираз для радіуса R, одержимо
 .
.
Обчислення.
 м = 11,8 мм.
м = 11,8 мм.
Відповідь: R = 11,8 м.
| Приклад 4. Коротка котушка, що містить 1000 витків, рівномірно обертається з частотою 10 об/с відносно осі, що лежить у площині котушки і перпендикулярна до ліній однорідного магнітного поля з індукцією 0,04 Тл (рис. 4.3). Визначити миттєве значення ЕРС індукції для тих моментів часу, коли площина котушки складає кут 600 з лініями поля. Площа котушки дорівнює 100 см2. |  Рис. 4.3. Рис. 4.3. |
Дано: N = 103, n = 10 об/с, B = 0,04 Тл, S = 10-2 м2.
Знайти: 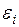 .
.
Розв’язок. Миттєве значення ЕРС індукції 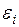 визначається основним рівнянням електромагнітної індукції Фарадея-Максвелла
визначається основним рівнянням електромагнітної індукції Фарадея-Максвелла
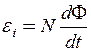 .
.
При обертанні котушки магнітний потік змінюється за законом  . Підставляючи вираз магнітного потоку у формулу для
. Підставляючи вираз магнітного потоку у формулу для 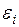 і диференціюючи за часом, знайдемо
і диференціюючи за часом, знайдемо
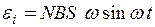 .
.
З огляду на те, що кутова швидкість  пов’язана з частотою обертання n і що кут
пов’язана з частотою обертання n і що кут  , одержимо
, одержимо
 .
.
Зробимо обчислення.
 В.
В.
Відповідь:  В.
В.
Приклад 5. Прямолінійний провідник, довжиною 1,2 м, з’єднаний із джерелом струму, ЕРС якого 24 В и внутрішній опір 0,5 Ом. Провідник знаходиться в однорідному магнітному полі з індукцією 0,8 Тл. Знайти струм у колі, якщо провідник рухається перпендикулярно лініям індукції поля з швидкістю 12,5 м/с. У скільки разів зміниться величина струму в колі, якщо провідник зупиниться? Опір усього зовнішнього кола прийняти за 2,5 Ом. Магнітним полем струму у провіднику знехтувати.
Дано: l = 1,2 м; 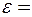 24 В; r = 0,5 Ом; R = 2,5 Ом; B = 0,8 Тл; 24 В; r = 0,5 Ом; R = 2,5 Ом; B = 0,8 Тл;  12,5 м/с. Знайти: 12,5 м/с. Знайти:  Розв’язок. Сила струму в провіднику визначається ЕРС джерела і різницею потенціалів, що виникає на кінцях провідника при його русі в напрямку, перпендикулярному до ліній магнітної індукції, тобто Розв’язок. Сила струму в провіднику визначається ЕРС джерела і різницею потенціалів, що виникає на кінцях провідника при його русі в напрямку, перпендикулярному до ліній магнітної індукції, тобто |  Рис. 4.4. Рис. 4.4. |
 .
.
У залежності від напрямку руху провідника 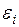 може або додавався до
може або додавався до  джерела, або відніматися. Тоді
джерела, або відніматися. Тоді
 А;
А;  А;
А;  А.
А.
Якщо провідник зупиниться, то 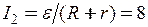 А. Таким чином, при зупинці провідника струм або збільшується в 2 рази, або зменшується в 1,5 рази.
А. Таким чином, при зупинці провідника струм або збільшується в 2 рази, або зменшується в 1,5 рази.
Приклад 6. Дротяна квадратна рамка із стороною 5 см і опором 10 Ом знаходиться в однорідному магнітному полі з індукцією 40 мТл. Нормаль до площини рамки складає кут 300 з лініями магнітної індукції. Визначити заряд, що пройде по рамці, якщо магнітне поле виключити.
Дано: a = 5?10–2 м, R = 10–2 Ом, В = 4?10–2 Тл,  = 300.
= 300.
Знайти: q.
Розв’язок. При вимиканні магнітного поля внаслідок зміни магнітного потоку в рамці наводиться ЕРС індукції  , яка викликає індукційний струм. Відповідно до закону Ома для повного кола
, яка викликає індукційний струм. Відповідно до закону Ома для повного кола
 або
або  .
.
З урахуванням того, що  запишемо
запишемо  .
.
Проінтегрувавши цей вираз, знайдемо
 або
або  .
.
За умовою задачі Ф2 = 0, а  і S = a 2 , томузапишемо
і S = a 2 , томузапишемо
 .
.
Зробимо обчислення.
 Кл.
Кл.
Відповідь: q = 8,67·10-3 Кл.
Приклад 7. Виток радіусом 2 см, по якому тече струм у 10 А, вільно встановився в однорідному магнітному полі з індукцією 1,5 Тл. Лінії індукції перпендикулярні до площини витка. Визначити роботу зовнішніх сил при повороті витка на кут 900 навколо осі, що збігає з діаметром витка.
Дано: I = 10 A; B = 1,5 Тл; r = 0,02 м;  = 900.
= 900.
Знайти: А.
Розв’язок. На виток зі струмом діє обертовий момент 
 , де магнітний момент
, де магнітний момент  .
.
У початковому положенні, відповідно до умови задачі, виток вільно установився в магнітному полі, отже, вектори  і
і  збігаються за напрямками, тобто
збігаються за напрямками, тобто  і М = 0.
і М = 0.
При дії зовнішніх сил виток виходить з початкового положення. При цьому зовнішні сили виконують роботу проти цього моменту, що є перемінним і залежить від кута повороту 
 або
або  .
.
Проінтегрувавши цей вираз, знайдемо роботу, виконану при повороті витка на кінцевий кут 
 .
.
Зробимо обчислення.
 Дж.
Дж.
Відповідь: А = 18,84·10-3 Дж.
Приклад 8. Соленоїд із сердечником з немагнітного матеріалу містить 1200 витків проводу, що щільно прилягають один до одного. При силі струму 4 А магнітний потік дорівнює 6 мкВб. Визначити індуктивність соленоїда і енергію магнітного поля соленоїду.
Дано: N = 1200; I = 4 A; Ф = 6·10–6 Вб.
Знайти: L, Wm.
Розв’язок. Індуктивність пов’язана з потокозчепленням і силою струму співвідношенням
 .
.
Враховуючи, що 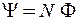 , то
, то  .
.
Енергія магнітного поля соленоїда 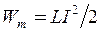 .
.
Підставивши вираз для індуктивності, одержимо
 .
.
Зробимо обчислення.
 Гн = 1,8 мГн.
Гн = 1,8 мГн.
 Дж = 14,4 мДж.
Дж = 14,4 мДж.
Відповідь: L = 1,8·10-3 Гн = 1,8 мГн; Wm = 1,44·10-2 Дж = 14,4 мДж.
Приклад 9. Матеріальна точка масою 10 г виконує коливання з періодом 1 с. Початкова фаза коливань 300. Визначити амплітуду коливань, максимальні швидкість і прискорення точки, що коливається, а також найбільше значення сили, що діє на точку, якщо максимальна кінетична енергія дорівнює 0,02 Дж.
Дано: m = 10–2 кг, Т = 1 с,  , Wk max = 0,02 Дж.
, Wk max = 0,02 Дж.
Знайти: А,  , a max.
, a max.
Розв’язок. Повна енергія точки, що коливається, дорівнює сумі кінетичної і потенціальної енергії; вона дорівнює максимальній кінетичній або максимальній потенційній енергії. Повна енергія гармонічного коливання визначається формулою  , звідки
, звідки
 .
.
З огляду на те, що  , одержимо
, одержимо
 м.
м.
Запишемо рівняння гармонічних коливань
 ,
,
де А = 0,32 м, 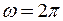 с–1,
с–1,  .
.
Швидкість визначається як перша похідна від зміщення за часом  , а
, а  м/с (з урахуванням того, що
м/с (з урахуванням того, що  ).
).
Прискорення – перша похідна від швидкості за часом
 .
.
Припускаючи, що  , знайдемо
, знайдемо
 = 12,62 м/с2.
= 12,62 м/с2.
Частинка робить гармонічні коливання під дією квазіпружної сили  , де k – коефіцієнт квазіпружної сили, х – зміщення точки, що коливається. Сила буде мати максимальне значення при зміщенні x max, яке дорівнює амплітуді
, де k – коефіцієнт квазіпружної сили, х – зміщення точки, що коливається. Сила буде мати максимальне значення при зміщенні x max, яке дорівнює амплітуді
 .
.
Коефіцієнт k зв’яжемо з періодом коливань
 .
.
Тоді
 ;
;
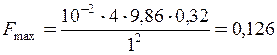 Н.
Н.
Відповідь:  м/с;
м/с;  м/с2;
м/с2; 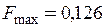 Н.
Н.
Приклад 10. Точки, що коливаються, віддалені від джерела коливань на відстань 1 м і 1,21 м у напрямку поширення хвилі. Різниця фаз коливань  /4, частота коливань джерела 200 с–1. Визначити довжину хвилі і швидкість її поширення.
/4, частота коливань джерела 200 с–1. Визначити довжину хвилі і швидкість її поширення.
Дано: х 1 = 1 м; х 2 = 1,21 м,  ,
,  =2·102 с–1.
=2·102 с–1.
Знайти:  ,
,  .
.
Розв’язок. З рівняння хвилі, що біжить, для коливання в точках х 1 і х 2 можна записати
 ,
,
 .
.
Знайдемо різницю фаз коливань  .
.
З огляду на те, що 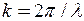 , одержимо
, одержимо  , звідки
, звідки
 ;
;  м.
м.
Швидкість поширення хвилі
 м/с.
м/с.
Відповідь:  м;
м; 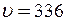 м/с.
м/с.
Приклад 11. Різниця потенціалів на обкладках конденсатора в коливальному контурі змінюється з часом за законом  . Електроємність конденсатора 0,5 мкФ. Визначити період власних коливань, індуктивність, енергію контуру і максимальну силу струму, що тече в котушці індуктивності.
. Електроємність конденсатора 0,5 мкФ. Визначити період власних коливань, індуктивність, енергію контуру і максимальну силу струму, що тече в котушці індуктивності.
Дано: U = 100sin1000  t; С = 0,5?10–6 Ф.
t; С = 0,5?10–6 Ф.
Знайти: Т, L, W, I max.
Розв’язок. Напруга на обкладках конденсатора змінюється за гармонічним законом  , де U 0 – амплітудне (максимальне) значення напруги;
, де U 0 – амплітудне (максимальне) значення напруги;  – власна циклічна частота коливань, що пов’язана з періодом коливань
– власна циклічна частота коливань, що пов’язана з періодом коливань  .
.
Звідси  с.
с.
З формули Томсона для періоду власних коливань у контурі знайдемо індуктивність  , тому
, тому
 ;
;  Гн = 0,2 Гн.
Гн = 0,2 Гн.
Енергія контуру – це сума електричної  і магнітної
і магнітної 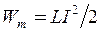 енергій, і дорівнює максимальній енергії поля конденсатора
енергій, і дорівнює максимальній енергії поля конденсатора 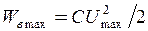 або максимальній енергії котушки індуктивності
або максимальній енергії котушки індуктивності 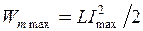 .
.
W = 0,5·10-6·1002/2 = 2,5·10-3 Дж.
Знаючи повну енергію, можна визначити максимальну силу струму, що протікає в котушці
 ;
;  А.
А.
Відповідь: T = 0,002 с;  Гн; W = 2,5·10-3 Дж; I max = 0,15 А.
Гн; W = 2,5·10-3 Дж; I max = 0,15 А.
Приклад 12. Відстань між двома когерентними джерелами 0,9 мм. Джерела посилають монохроматичне світло з довжиною хвилі 640 нм на екран, розташований від них на відстані 3,5 м. Визначити число світлих смуг на 1 см довжини. Дано: d = 9?10–4 м,  = 6,4?10–7 м, L = 3,5 м, х = 10–2 м. = 6,4?10–7 м, L = 3,5 м, х = 10–2 м. |  Рис. 4.5. Рис. 4.5. |
Знайти: k / х.
Розв’язок. У точці О на екрані (рис. 4.5) буде максимальна освітленість. Ця точка рівновіддалена від обох джерел S1 і S2, тому різниця ходу променів S1O і S2O дорівнює нулю. У довільній точці О1 максимум освітленості буде спостерігатися, якщо різниця ходу променів дорівнює цілому числу довжин хвиль  , де k – номер світлої смуги. З рисунка видно, що
, де k – номер світлої смуги. З рисунка видно, що  , звідки
, звідки  і тому
і тому  . Звідси число світлих інтерференційних смуг, що припадають на одиницю довжини
. Звідси число світлих інтерференційних смуг, що припадають на одиницю довжини
 .
.
Підставляючи числові дані, одержимо
 м-1.= 4 см-1.
м-1.= 4 см-1.
Відповідь:  см-1.
см-1.
| Приклад 13. На скляний клин нормально до його грані падає монохроматичне світло з довжиною хвилі 0,6 мкм. Число інтерференційних смуг, що припадає на 1 см, дорівнює 10. Визначити заломлюючий кут клина (n = 1,5). |  Рис. 4.6. Рис. 4.6. |
Дано: n = 1,5; i = 00;  = 6?10–7 м; l = 10–2 м; N = 10.
= 6?10–7 м; l = 10–2 м; N = 10.
Знайти:  .
.
Розв’язок. Паралельний пучок променів, падаючи нормально до грані клина, відбивається як від верхньої, так і від нижньої граней. Ці промені когерентні і тому спостерігається стійка інтерференційна картина при їхньому накладенні. Різниця ходу променів визначається формулою
 . (1)
. (1)
Темні смуги спостерігаються на тих ділянках клина, для яких різниця променів кратна непарному числу напівхвиль
 . (2)
. (2)
Дорівнявши праві частини рівнянь (1) і (2) одержимо
 .
.
Оскільки кут падіння i = 0 (sin i = 0), то  , звідки
, звідки  , де dk – товщина клина в тому місці, де спостерігається темна смуга, що відповідає номеру k. Сусідня темна смуга з номером (k + 1), що відповідає товщині клина dk +1, знаходиться на відстані l / N. (рис. 4.6),
, де dk – товщина клина в тому місці, де спостерігається темна смуга, що відповідає номеру k. Сусідня темна смуга з номером (k + 1), що відповідає товщині клина dk +1, знаходиться на відстані l / N. (рис. 4.6), 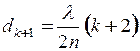 .
.
На рисунку бачимо, що пошукуваний кут (через його малість, можна вважати  )
)  , або
, або  .
.
Підставивши числові дані, одержимо
 рад.;
рад.;  .
.
Відповідь:  .
.
| Приклад 14. На дифракційну ґратку нормально падає паралельний пучок променів з довжиною хвилі 500 нм. На екрані, паралельному дифракційній ґратці і віддаленому від неї на 1 м, спостерігається дифракційна картина. Відстань між максимуму першого порядку на екрані дорівнює 20,2 см. Визначити сталу дифракційної ґратки, число штрихів на 1 см, число максимумів, що дає дифракційна ґратка, макси- |  Рис. 4.7. Рис. 4.7. |
мальний кут відхилення променів, що відповідає останньому дифракційному максимуму.
Дано: λ = 5?10–7 м, L = 1 м, k = 1, l = 0,202 м.
Знайти: d, N, k max,  .
.
Розв’язок. Умова максимуму при дифракції від ґратки має вид  . У цій задачі порядок спектра k = 1, а
. У цій задачі порядок спектра k = 1, а  (зазначене наближення має місце, тому що
(зазначене наближення має місце, тому що 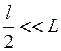 ). Тоді
). Тоді  , звідки стала ґратки
, звідки стала ґратки  . Підставивши числові дані, одержимо
. Підставивши числові дані, одержимо
 м.
м.
Число штрихів на одиниці довжини знайдемо з формули
 м-1 = 2020 см-1.
м-1 = 2020 см-1.
Для визначення числа максимумів, яке дає дифракційна ґратка, обчислимо максимальне значення k, яке визначимо з тієї умови, що максимальний кут відхилення променів дифракційними ґратками не може перевищувати 900.
 .
.
Оскільки число максимумів k повинно бути тільки цілим числом, то k = 9 (k не може прийняти значення 10, тому що при цьому  ).
).
Підрахуємо число максимумів, яке дає дифракційна ґратка: вліво і вправо від центрального максимуму, для котрого k = 0, буде спостерігатися однакове число максимумів, що дорівнює k max, тобто всього 2 k max. З огляду на центральний (нульовий) максимум, одержимо загальне число максимумів M = 2 k max + 1, тобто M = 2?9+1 = 19.
Найбільший кут відхилення променів, що відповідає останньому дифракційному максимуму знайдемо у такий спосіб
 , тобто
, тобто 
Відповідь: d = 4,95·10-6 м; N = 2020 см-1;  ;
; 
Приклад 15. Природне світло падає на поліровану поверхню скляної пластини, зануреної в рідину. Відбитий від пластини промінь утворює кут 970 з падаючим променем. Визначити показник заломлення рідини, якщо відбитий промінь максимально поляризований.
Дано: i б = 970/2; n 2 = 1,5.
Знайти: n 1.
Розв’язок. Відповідно до закону Брюстера відбитий промінь буде максимально поляризований, якщо тангенс кута падіння чисельно дорівнює відносному показникові заломлення;  , звідки
, звідки  .
.
 .
.
Відповідь: n 1 = 1,33.
Приклад 16. Який кут утворюють площини поляризації двох ніколей, якщо світло, що вийшло з другого ніколя, було ослаблене у 5 разів. Врахувати, що поляризатор поглинає 10 %, а аналізатор 8 % падаючого на них світла.
Дано: k 1 = 0,1; k 2 = 0,08; n = I 0/ I 2 = 5.
Знайти: 
Розв’язок. Природний промінь світла, падаючи на грань призми Ніколя, зазнає подвійного променезаломлення, у результаті чого виникають два промені: звичайний і незвичайний. Обидва промені поляризовані у взаємно перпендикулярних площинах, інтенсивність їх однакова і дорівнює половині інтенсивності природного світла. З урахуванням поглинання інтенсивність світла, що пройшло через поляризатор 
 , де I 0 – інтенсивність природного світла, що падає на перший ніколь.
, де I 0 – інтенсивність природного світла, що падає на перший ніколь.
Поляризований промінь, потрапляючи на другу призму (аналізатор), знову випробує поглинання. Крім того, інтенсивність цього променя зменшується через розбіжність площин поляризації поляризатора й аналізатора. Зменшення інтенсивності визначається законом Молюса 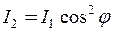 .
.
З урахуванням втрат інтенсивності світла в аналізаторі, одержимо
 ,
,
звідки
 .
.
Зробимо обчислення.
 , тобто
, тобто  .
.
Відповідь:  .
.
КОНТРОЛЬНА РОБОТА № 4
401. Якої довжини повинен бути провідник кругового витка, щоб при струмі в 10 А магнітна індукція в центрі витка дорівнювала
1,26·104 Тл.
402. Перпендикулярно до площини кільцевого провідника радіусом
40 см проходить ізольований довгий провідник так, що він торкається кільця. Сила струму у провіднику 20 А. Знайти індукцію магнітного поля в центрі кільця.
403. Чому дорівнює сила струму, що проходить по периметру правильного шестикутника із стороною 20 см, якщо в його центрі індукція магнітного поля 12,56·10-6 Тл?
404. У точці, віддаленій від двох прямолінійних паралельних провідників на відстань 10 см, магнітна індукція поля дорівнює 20 мкТл. По одному з провідників тече струм 0,5 А. Який струм тече по другому провіднику, якщо він віддалений від першого на 10 см?
405. Якої сили струм необхідно пропустити по провіднику, вигнутому у формі квадрата, щоб магнітна індукція в центрі дорівнювала
10-5 Тл? Сторона квадрата 10 см.
406. Два кільцевих провідники радіусами 0,8 і 0,5 м розташовані таким чином, що центри їх збігаються, а площини утворюють 900. Визначити індукцію магнітного поля у загальному центрі кілець, якщо струми, що течуть по кільцях, дорівнюють відповідно 32 А і
15 А.
407. По провіднику, вигнутому у формі кола, тече струм. Напруженість магнітного поля в центрі кола 50 А/м. Не змінюючи сили струму в провіднику, йому надали форму квадрата. Визначити індукцію магнітного поля в точці перетину діагоналей цього квадрата.
408. Якої густини струм потрібно пропускати по котушці довжиною
15 см, щоб індукція магнітного поля в її середині дорівнювала 25·10-5 Тл, якщо діаметр дроту 1 мм, а число витків котушки 100.
409. Прямий провідник зігнутий у формі прямокутника із сторонами 20 см і 30 см. Визначити силу струму в провіднику, якщо в точці перетину діагоналей магнітна індукція дорівнює 50 мкТл.
410. Де і на скільки індукція магнітного поля більша: у центрі квадратного провідника із стороною 5 см або в центрі кругового провідника, отриманого з того ж проводу, якщо по провідниках тече струм у 5 А?
411. На каркас довжиною 20 см і діаметром 3 см намотано 150 витків дроту. Через середину каркасу в напрямку одного з його діаметрів проходить мідний провідник із струмом у 5 А. Вважаючи магнітне поле в середній частині соленоїда однорідним, визначити силу, з якою воно діє на ділянку провідника всередині каркасу, якщо струм у соленоїді дорівнює 1 А.
412. Визначити індукцію магнітного поля між полюсами електромагніту, якщо провідник вагою 0,5 Н на 1 м довжини при струмі в ньому 10 А знаходиться в полі електромагніту у завислому стані.
413. Рамка гальванометра довжиною 4 см і шириною 1,5 см, що містить 200 витків тонкого дроту, знаходиться в магнітному полі напруженістю 105 А/м. Площина рамки паралельна до напрямку поля. Який обертовий момент діє на рамку, коли по її обмотці тече струм 1 мА? Який магнітний момент рамки при цьому струмі?
414. Під впливом однорідного магнітного поля в ньому рухається з прискоренням 0,2 м/с2 прямолінійний алюмінієвий провідник із площею поперечного перетину 1 мм2. По провіднику тече струм силою 9 А и його напрям перпендикулярний до індукції поля. Обчислити цю індукцію.
415. Два прямолінійних довгих провідники розташовані паралельно один до одного на відстані 10 см. По провідниках течуть струми в 20 А і 30 А в одному напрямку. Яку роботу треба зробити (на одиницю довжини провідників), щоб розсунути провідники до 20 см?
416. Нормаль до площини рамки складає кут 300 з напрямком однорідного магнітного поля. Під яким кутом установилася рамка відносно поля, якщо обертовий момент, що діє на рамку, зменшився в 3 рази?
417. Напруженість магнітного поля 50 А/м. У полі знаходиться плоска рамка площею поперечного перерізу 10 см2, що вільно обертається. Спочатку площина рамки збігалася з напрямком індукції поля. Потім по рамці короткочасно пропустили струм у 1 А, і рамка одержала кутове прискорення 100 см-2. Вважаючи умовно обертовий момент постійним, знайти момент інерції рамки.
418. Виток радіусом 20 см, по якому тече струм 50 А, вільно установився в однорідному магнітному полі з індукцією 12,56·10-4 Тл. Виток повернули щодо діаметра на кут 300. Визначити виконану при цьому роботу.
419. Круговий контур поміщений в однорідне магнітне поле так, що площина контуру перпендикулярна до силових ліній поля. Індукція магнітного поля дорівнює 0,2 Тл. По контуру тече струм силою 2 А. Радіус контуру 2 см. Яку роботу треба виконати, щоб повернути контур на 900 навколо осі, що співпадає з діаметром контуру?
420. Яка потужність необхідна для того, щоб провідник довжиною 20 см переміщувати зі швидкістю 5 м/с перпендикулярно до магнітного поля напруженістю 5·105 А/м, якщо по провіднику тече струм 10 А?
421. Електрон, що пройшов прискорюючу різницю потенціалів у 500 В, попадає в однорідне магнітне поле і рухається по колу радіусом 10 см. Визначити величину індукції магнітного поля, якщо швидкість електрона перпендикулярна до силових ліній.
422. Магнітне поле з індукцією 5·10-4 Тл спрямоване перпендикулярно до електричного поля з напруженістю 10 В/см. Пучок електронів влітає в простір, де розташовані ці поля, причому швидкість електронів перпендикулярна до площини, у якій лежать вектори 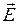 і
і  . Знайти швидкість електронів, якщо при одночасній дії обох полів пучок електронів не випробує відхилення, і радіус кривизни за умови включення одного магнітного поля.
. Знайти швидкість електронів, якщо при одночасній дії обох полів пучок електронів не випробує відхилення, і радіус кривизни за умови включення одного магнітного поля.
423. Частота обертання електрона в магнітному полі по круговій орбіті дорівнює 2,8·1010 Гц. Визначити індукцію магнітного поля.
424. Електрон влітає в однорідне магнітне поле перпендикулярно до силових ліній. Швидкість електрона 4·107 м/с. Індукція магнітного поля дорівнює 10-3 Тл. Знайти тангенціальне і нормальне прискорення електрона у магнітному полі?
425. Заряджена частинка, проходячи прискорюючу різницю потенціалів у 200 В, влетіла в схрещені під прямим кутом електричне і магнітне поля, рухаючись при цьому перпендикулярно до обох полів. Напруженість електричного поля 12 кВ/м, індукція магнітного поля 0,6 Тл. Знайти питомий заряд частинки.
426. Електрон рухається в однорідному магнітному полі з індукцією
10-3 Тл так, що його швидкість складає кут 300 з напрямком поля. Визначити радіус витка траєкторії електрона і відстань, пройдену ним уздовж силових ліній за час, що дорівнює періоду, якщо швидкість електрона складає 2,5·106 м/с.
427. В однорідне магнітне поле з індукцією 0,01 Тл перпендикулярно до силових ліній влетів електрон з енергією 30 кеВ. Визначити частоту і радіус кривизни траєкторії електрона.
428. Електрон пройшов прискорюючу різницю потенціалів у 800 В і влетів в однорідне магнітне поле з індукцією 47 мТл. Крок гвинтової лінії 6 см. Визначити радіус гвинтової лінії.
429. На фотографії, отриманій у камері Вільсона, поміщеній в однорідне магнітне поле, траєкторія електрона являє собою дугу кола радіусом 10 см. Індукція магнітного поля 10-2 Тл. Знайти енергію електрона (виразити в електрон-вольтах).
430. Протон влетів в однорідне магнітне поле під кутом 600 до напрямку ліній поля і рухається по спіралі, радіус якої 2,5 см. Індукція магнітного поля 0,05 Тл. Знайти кінетичну енергію протона.
431. Прямолінійний провідник зі струмом 300 А і масою 40 г переміщується під дією поля і перетинає магнітний потік 10 Вб. Вважаючи, що провідник переміщується вільно і перпендикулярно до поля визначити швидкість, що набувається провідником.
432. На довгий каркас діаметром 5 см покладено одношарову обмотку з проводу діаметром 0,2 мм. Визначити магнітний потік, створений таким соленоїдом при силі струму 5 А.
433. Знайти магнітний потік у соленоїді, що містить 500 витків/м, якщо його діаметр 10 см, а сила струму, що протікає в ньому, 1 А.
434. Знайти магнітний потік через соленоїд, якщо його довжина 50 см, а магнітний момент 19,9 А·м2. Витки соленоїда щільно прилягають один до одного.
435. В однорідному магнітному полі з напруженістю 8·104 А/м поміщена квадратна рамка, сторона якої 4 см. Площина рамки складає кут 600 з напрямком магнітного поля. Визначити магнітний потік, що пронизує рамку.
436. Скільки ампер-витків буде потрібно для створення магнітного потоку в 4,2 Вб у соленоїді із залізним сердечником довжиною
120 см і площею поперечного перетину 3 см2? Скористатися графіком 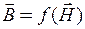 (рис. 4.8).
(рис. 4.8).
437. По довгому прямолінійному провіднику тече струм силою 10 А. Провідник знаходиться в площині контуру, що має форму квадрата із стороною20 см. Найближча до провідника сторона квадрата
| паралельна до провідника і знаходиться на відстані 10 см від нього. Знайти потік магнітної індукції через контур. 438. В однорідному магнітному полі перпендикулярно до ліній індукції розташований плоский контур площею 100 см2. Підтримуючи в контурі постійну силу струму 50 А, його перемістили з поля в |  Рис. 4.8. Рис. 4.8. |
ділянку простору, де поле відсутнє. Визначити індукцію магнітного поля, якщо при переміщення контуру була виконана робота 0,4 Дж.
439. Потік магнітної індукції через площу поперечного перерізу соленоїда (без сердечника) дорівнює 1 мкВб. Довжина соленоїда 12,5 см. Визначити магнітний момент цього соленоїда.
440. Рамка площею 16 см2 обертається в однорідному магнітному полі, роблячи 2 об/с. Вісь обертання знаходиться у площині рамки і перпендикулярна до силових ліній магнітного поля, напруженість якого 7,96·104 А/м. Знайти залежність магнітного потоку, що пронизує рамку, від часу і найбільшого значення магнітного потоку.
441. Кругла рамка, що має 200 витків і площу 100 см2, рівномірно обертається в однорідному магнітному полі з індукцією 0,03 Тл навколо осі, перпендикулярної до поля і співпадаючою з діаметром рамки. Обчислити частоту обертання рамки, якщо максимальна сила струму, що індукується в ній при її опорі 20 Ом складає 0,04 А.
442. В однорідному магнітному полі з індукцією 0,01 Тл під кутом 300 до поля розташована мідна рамка з стороною 0,5 м. Рамку повернули перпендикулярно до поля. Який заряд пройшов по рамці, якщо діаметр проводу 0,2 мм?
443. Виток радіусом 1 см знаходиться в магнітному полі напруженістю 20 кА/м. Площина витка перпендикулярна до поля. Визначити опір цього витка, якщо по ньому протікає заряд 1 мКл при зменшенні струму до нуля.
444. Металевий стрижень довжиною 2 м обертається з постійною частотою 20 об/с навколо осі, що проходить через один з кінців стрижня паралельно до силових ліній магнітного поля. Знайти різницю потенціалів, що виникає на кінцях стрижня, якщо індукція поля дорівнює 12,56·10-5 Тл.
445. Прямий провідник довжиною 20 см і опором 0,1 Ом рухається перпендикулярно до магнітного поля. При замиканні провідника йде струм 5 мА. Визначити швидкість руху провідника, якщо магнітна індукція поля 0,5 Тл.
446. Соленоїд перетином 5 см2 містить 1200 витків. Індукція магнітного поля усередині соленоїда при силі струму 2 А дорівнює 0,01 Тл. Визначити індуктивність соленоїда.
447. На залізний сердечник перетином 5 см2 і довжиною 30 см намотаний соленоїд, що містить 500 витків мідного дроту перетином 1 мм2. Чому дорівнює індуктивність соленоїда при підключенні його до акумулятора з ЕРС 1,26 В? Внутрішнім опором акумулятора і проводів, що підводять, знехтувати. Скористатися графіком 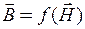 (рис. 4.8).
(рис. 4.8).
448. Соленоїд з одношаровою обмоткою, витки якої щільно прилягають одна до одної, має довжину 20 см і площу поперечного перерізу
5 см2. Обмотка виконана з проводу діаметром 0,1 мм, сердечник відсутній. З якою швидкістю слід змінювати силу струму в обмотці, щоб у соленоїді виникла ЕРС самоіндукції 5 В?
449. Число витків соленоїда без сердечника 400, його довжина 20 см, поперечний перетин 4 см2, опір обмотки 16 Ом. Яка кількість електрики індукується у соленоїді, якщо сила струму зросла в ньому від 0 до 10 А?
450. З якого числа витків дроту складається одношарова обмотка котушки, індуктивність якої 0,001 Гн? Діаметр котушки 4 см, діаметр дроту 0,6 мм. Витки щільно прилягають один до одного.
451. На довгий залізний сердечник радіусом 1 см намотаний одношаровий соленоїд, що містить 10 витків на кожному сантиметрі довжини. Через який час в обмотці виділиться кількість теплоти, що дорівнює енергії магнітного поля у сердечнику, якщо вона підключена до джерела постійної напруги? Прийняти  .
.
452. При силі струму 10 А в обмотці соленоїда, яка складається з 2000 витків, магнітний потік через перетин соленоїда дорівнює
2·10-3 Вб. Визначити енергію магнітного поля соленоїда.
453. Діаметр тороїда (по середній лінії) 90 см. Тороїд містить 2000 витків і має площу перетину 20 см2. Обчислити енергію магнітного поля тороїда при силі струму 5 А. Вважати магнітне поле однорідним. Сердечник виконаний з немагнітного матеріалу.
454. Визначити індуктивність соленоїда, що містить 1000 витків, якщо магнітний потік, утворений струмом силою 1 А, дорівнює 0,5 мВб. Яка енергія магнітного поля соленоїда?
455. Плоский контур з струмом 50 А вільно установився в магнітному полі. Яку роботу необхідно виконати, щоб повернути контур площею 200 см2 на 300 навколо осі, що лежить у його площині, якщо об'ємна густина енергії магнітного поля складає 2·106 Дж/м3?
456. Індуктивність суцільної одношарової котушки довжиною 60 см, намотаної на каркас діаметром 3 см, дорівнює 0, 5 мГн. Визначити діаметр проводу і число витків на одиницю довжини соленоїда. Чому дорівнює густина енергії магнітного поля при силі струму 0,1 А?
457. При якій силі струму в довгому прямолінійному провіднику об'ємна густина енергії магнітного поля в точці, розташованій на відстані 5 см від провідника буде дорівнювати 1 мДж/м3?
458. Соленоїд має довжину 1 м і перетин 20 см2. При деякій силі струму, що протікає по обмотці, у соленоїді створюється магнітний потік, що дорівнює 80 мкВб. Знайти енергію магнітного поля соленоїда?
459. По провіднику, вигнутому у формі кільця радіусом 20 см, що містить 500 витків, тече струм силою 1 А. Визначити об'ємну густину енергії магнітного поля в центрі кільця.
460. При індукції 1 Тл, густина енергії магнітного поля у залізі
200 Дж/м3. Яка магнітна проникність заліза за цих умов? Скористатися графіком  (рис. 4.8).
(рис. 4.8).
461. Вантаж вагою 40 Н підвішено на кінці пружини, коливаючись гармонічно, робить 10 коливань за 5 с. Повна енергія коливального руху вантажу у початковий момент була 2 Дж. На скільки відтягнули вантаж від положення рівноваги?
462. Знайти відношення кінетичної енергії точки, що робить гармонічні коливання, до її потенційної енергії для моменту часу, коли зміщення точки від положення рівноваги складає половину амплітуди.
463. Матеріальна точка коливається гармонічно. Амплітуда коливань 5 см, циклічна частота 2 с-1, початкова фаза дорівнює нулю. Визначити швидкість, яку має точка в момент, коли її прискорення дорівнює 4 см/с2.
464. Диск радіусом 24 см коливається біля горизонтальної осі, що проходить через середину одного з радіусів перпендикулярно до площини диска. Визначити наведену довжину і період коливань такого маятника.
465. Через який час енергія коливань камертона з частотою 600 Гц зменшиться в 106 разів, якщо логарифмічний декремент затухання 0,0008?
466. Рівняння незатухаючих коливань має вигляд х = 4sin600 t см. Знайти зміщення від положення рівноваги точки, яка знаходиться на відстані 75 см від джерела коливань. Швидкість поширення коливань 300 м/с.
467. Максимальна енергія магнітного поля коливального контуру 1 мДж при силі струму 0,8 А. Чому дорівнює період коливань контуру, якщо максимальна різниця потенціалів на обкладках конденсатора 1200 В?
468. Період коливань струму в контурі, що складається з індуктивності і ємності, дорівнює 10-5 с. Якою буде максимальна сила струму в котушці, якщо максимальна різниця потенціалів на обкладках конденсатора 900 В? Максимальна енергія електричного поля 9·10-4 Дж.
469. Визначити частоту коливань і максимальну напругу на конденсаторі в коливальному контурі, якщо індуктивність котушки 500 мкГн, максимальна сила струму 2 А, а ємність конденсатора 6 нФ.
470. Котушка, індуктивність якої 3·10-5 Гн, приєднана до плоского конденсатора з площею пластин 100 см2. Відстань між пластинами 0,1 мм. Чому дорівнює діелектрична проникність середовища, яке заповнює простір між пластинами, якщо контур резонує на хвилю довжиною 750 м?
471. Яка відстань між 20-м і 21-м світлими кільцями Ньютона, якщо відстань між другим і третім дорівнює 1 мм, а спостереження ведеться у відбитому світлі?
472. Оптична сила лінзи (n = 1,5) 0,5 дптр. Лінза опуклою стороною лежить на скляній пластинці. Визначити радіус сьомого темного кільця Ньютона у прохідному світлі з довжиною хвилі 0,5 мкм.
473. Між скляною пластинкою і плоскоопуклою лінзою, що лежить на ній, знаходиться рідина. Який показник її заломлення, якщо при спостереженні у відбитому світлі з довжиною хвилі 600 нм радіус десятого темного кільця Ньютона 2,1 мм? Радіус кривизни лінзи 1 м.
474. Біле світло, що падає нормально на мильну плівку (n = 1,33) у відбитому світлі дає інтерференційний максимум на довжині хвилі 630 нм, а найближчий до нього інтерференційний максимум на довжині хвилі 450 нм. Визначити товщину плівки.
475. Дифракційна ґратка містить 100 штрихів на 1 мм довжини. Визначити довжину хвилі монохроматичного світла, що падає на ґратку нормально, якщо кут між двома спектрами першого порядку 80.
476. Спектри дифракційної ґратки, що має 100 штрихів на 1 мм, проектуються на екран, розташований паралельно до ґратки на відстані 1,8 м від неї. Визначити довжину хвилі світла, що падає нормально на ґратку, якщо відстань від другого спектрального максимуму до центральної світлої смуги в площині екрана склала 21,4 см.
477. На поверхню дифракційної ґратки нормально до неї падає монохроматичне світло. Стала дифракційної ґратки у 4,9 разів більша від довжини світлової хвилі. Знайти загальне число дифракційних максимумів, що теоретично можна спостерігати у даному випадку.
478. На непрозору пластинку з вузькою щілиною падає нормально монохроматична світлова хвиля ( нм). Кут відхилення променів, що відповідають другому дифракційному максимуму, дорівнює 200. Визначити ширину щілини.
нм). Кут відхилення променів, що відповідають другому дифракційному максимуму, дорівнює 200. Визначити ширину щілини.
479. У скільки разів слабшає світло, проходячи через два ніколя, площини поляризації яких складає кут 630, причому в кожному з ніколей губиться 10 % падаючого світла?
480. При переході променя світла з прозорого середовища у воду граничний кут заломлення виявився рівним 550. Під яким кутом на поверхню середовища повинен падати промінь, що йде у воді, щоб відбитий промінь був цілком поляризований?
 2015-10-22
2015-10-22 66441
66441
