Уравнения с разделяющимися переменными

Диффур 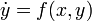назур с разделяющимися (отделяющимися) переменными, если его правая часть представима в виде 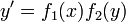. Тогда, в случае 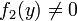, общим решением уравнения является .

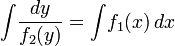ПРИМЕР: физических задач, приводящих к уравнениям с разделяющимися переменными - Охлаждение тела:

Пусть 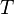— температура тела, 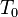— температура окружающей среды (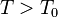). Пусть 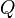— количество теплоты, — удельная теплоёмкость. Тогда количество теплоты, передаваемое окружающей среде до выравнивания температур, выражается формулой 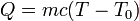, или, в дифф форме, .

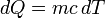С другой стороны, скорость отдачи тепла можно выразить в ви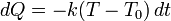де , где 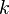— некий коэффициент пропорциональности. Исключаяиз этих двух уравнений 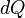, получаем уравнение с разделяющимися переменными:

.

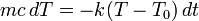Общее решение – семейство функций: .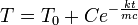

Виды решений ОДУ:

Общее решение ОДУ n -го порядка содержит N произвольных постоянных С_i, т.е. общее решение имеет вид:y=φ(x,C₁,C₂,…C_n)

Частное решение ОДУ получается из общего, если произвольным постоянным придать определенные значения.

Методы решения:

Теорема Коши; м Эйлера (получение приближенного решения ОДУ - аппроксимация производной), наиболее простой метод решения ОДУ. Обладает медленной сходимостью, поэтому чаще применяют методы более высокого порядка точности; мЭйлера-Коши, значение правой части итерационного уравнения заменяют средним арифметическим значением между f(x_i,y_i) и f(x_i+1,y_i+1), с получением неявной схемы; м Эйлера с пересчетом; м Эйлера с пересчетом с автоматическим выбором шага; м Рунге-Кутта; м прогноза и коррекции.

М Эйлера и его модиф варианты могут расс-ться как м Рунге-Кутта 1-го и 2-го порядков.

Повышение точности результатов: применяя разностные схемы повышенного порядка точности. Однако, такие схемы целесообразно применять лишь для уравнений с постоянными коэффициентами.

На практике для повышения точности применяют метод Рунге: проводятся повторные расчеты по одной разностной схеме с различными шагами. Уточненное решение в совпадающих при разных расчетах узлах строиться с помощью проведенной серии расчетов.