Задача 1. Звести формулу  до диз’юнктивної нормальної форми (ДНФ) та досконалої диз’юнктивної нормальної форми (ДДНФ).
до диз’юнктивної нормальної форми (ДНФ) та досконалої диз’юнктивної нормальної форми (ДДНФ).
Розв’язання. Використовуючи означення операцій “стрілка Пірса” та “штрих Шеффера”, маємо


 .
.
Для того, щоб побудувати ДДНФ застосуємо формулу розщеплення:

 .
.
Задача 2. Використовуючи теорему про диз’юнктивний розклад булевої функції, розкласти функцію  за змінними
за змінними  та
та  .
.
Розв’язання. За теоремою про диз’юнктивний розклад маємо:
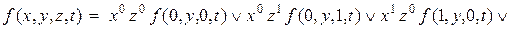

Обчислимо:
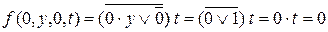 ;
;
 ;
;
 ;
;
 .
.
Підставивши отримані значення у формулу диз’юнктивного розкладу, маємо
 .
.
Задача 3. Нехай булева функція задана таблицею
 |  |  |  |
Побудувати ДДНФ та досконалу кон’юнктивну нормальну форму (ДКНФ) даної функції.
Розв’язання. Для побудови ДДНФ виділимо в таблиці ті рядки, для яких значення функції  на відповідному булевому наборі дорівнює 1. Виписавши елементарні кон’юнкції, які їм відповідають, маємо:
на відповідному булевому наборі дорівнює 1. Виписавши елементарні кон’юнкції, які їм відповідають, маємо:
 .
.
Для того, щоб побудувати ДКНФ для функції  , виділимо в таблиці ті рядки, в яких значення функції дорівнює нулю. Для кожного з цих булевих наборів будуємо відповідну елементарну диз’юнкцію. Маємо:
, виділимо в таблиці ті рядки, в яких значення функції дорівнює нулю. Для кожного з цих булевих наборів будуємо відповідну елементарну диз’юнкцію. Маємо:

 .
.
Задача 4. Скільки існує самодвоїстих функцій від  змінних?
змінних?
Розв’язання. Множина наборів, значення на яких визначають самодвоїсту функцію, містить  елементів (половина всіх можливих наборів). Оскільки булева функція на кожному наборі може приймати два значення 0 та 1, то існує
елементів (половина всіх можливих наборів). Оскільки булева функція на кожному наборі може приймати два значення 0 та 1, то існує  самодвоїстих функцій від
самодвоїстих функцій від  змінних.
змінних.
Задача 5. Довести, що на протилежних наборах самодвоїста функція приймає протилежні значення.
Розв’язання. Нехай  – самодвоїста функція, тобто
– самодвоїста функція, тобто
 .
.
Маємо
 .
.
Задача 6. Побудувати булеву функцію  , двоїсту до функції
, двоїсту до функції  .
.
Розв’язання. Замінимо в даній функції всі знаки  на
на  (двічі),
(двічі),  на
на  та 0 на 1. Використавши дужки для того, щоб порядок виконання операцій залишився тим же, маємо
та 0 на 1. Використавши дужки для того, щоб порядок виконання операцій залишився тим же, маємо
 .
.
Задача 7. Мінімізувати за допомогою методу Квайна булеву функцію
 .
.
За допомогою методу Петрика виписати всі тупикові ДНФ та вибрати серед них мінімальні.
Розв’язання. Виконавши всі можливі операції склеювання, отримаємо диз’юнкцію всіх можливих імплікант функції  (скорочену ДНФ):
(скорочену ДНФ):

 .
.
Очевидно, що операція поглинання не може бути застосованою до отриманої формули. Будуємо імплікантну таблицю.
 |  |  |  |  |  | ||
 |  | • | • | ||||
 |  | • | • | ||||
 |  | • | • | ||||
 |  | • | • | ||||
 |  | • | • | ||||
 |  | • | • | ||||
 |  |  |  | 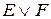 |  |
У таблиці відміченими є ті клітинки, для яких проста імпліканта, що маркує рядок, є власною частиною повної елементарної кон’юнкції, що маркує стовпчик (імпліканта поглинає відповідну повну елементарну кон’юнкцію). Сформуємо набори покриттів і випишемо мінімальні тупикові ДНФ.
Очевидно, що не існує таких наборів покриттів, у яких використовується одна чи дві прості імпліканти. В той же час існують два набори покриттів, у яких використовуються по три імпліканти (замість шести початкових):
ТДНФ  ; ТДНФ
; ТДНФ  .
.
Ці тупикові форми і будуть мінімальними.
Для того, щоб за допомогою методу Петрика виписати всі тупикові форми, поставимо у відповідність кожній простій імпліканті даної функції деяку літеру (ідентифікатор) – перший стовпчик таблиці. Кожному стовпчику приписується диз’юнкція літер, які відповідають тим рядкам, в яких у даному стовпчику стоїть значок “•” – останній рядок таблиці. Далі утворюємо кон’юнкцію цих диз’юнкцій:
 .
.
Це і буде формула покриття конституент одиниці простими імплікантами.
Перетворимо цю формулу до ДНФ, застосовуючи при цьому закони дистрибутивності, ідемпотентності, поглинання та комутативності. Маємо:





( поглинає
поглинає  та
та  ). Кожна елементарна кон’юнкція утвореної ДНФ відповідає одній тупиковій формі даної функції, тобто
). Кожна елементарна кон’юнкція утвореної ДНФ відповідає одній тупиковій формі даної функції, тобто
ТДНФ  ;
;
ТДНФ  ;
;
ТДНФ  ;
;
ТДНФ  ;
;
ТДНФ  .
.
Очевидно, що перші дві тупикові форми і будуть мінімальними.
A6
1. На інтерпретаціях № 2 та № 5 знайти істинносне значення функції  .
.
2. Чи буде функція  тотожно дорівнювати 0 чи 1?
тотожно дорівнювати 0 чи 1?
3. Нехай задана функція  .
.
a) Який порядковий номер цієї функції?
b) Застосовуючи тотожні перетворення, спростити формулу, яка задає  .
.
c) Розкласти функцію  за змінною
за змінною  .
.
d) Побудувати ДКНФ функції  .
.
e) Побудувати  . Чи буде функція
. Чи буде функція  самодвоїстою?
самодвоїстою?
4. Застосовуючи тотожні перетворення, привести функцію  до виду ДНФ, а потім ДДНФ.
до виду ДНФ, а потім ДДНФ.
5. Функція від трьох змінних набуває значень 1 на наборах № 1, 2, 4, 7. Побудувати ДДНФ і ДКНФ. З’ясувати, чи буде ця функція самодвоїстою.
6. З’ясувати, чи будуть повними системи функцій:
a)  ; b)
; b)  .
.
7. З’ясувати, які з елементарних кон’юнкцій, складених з двох змінних  та
та  , є імплікантами функції
, є імплікантами функції  . Чи будуть вказані імпліканти простими? Вказати прості імпліканти.
. Чи будуть вказані імпліканти простими? Вказати прості імпліканти.
8. За допомогою карт Карно мінімізувати булеві функції:
a)  ;
;
b)  .
.
9. Функція  приймає значення 1 на наборах: 010, 011, 100, 101 та 111. За допомогою методу Петрика знайти тупикові ДНФ та вибрати серед них мінімальні форми.
приймає значення 1 на наборах: 010, 011, 100, 101 та 111. За допомогою методу Петрика знайти тупикові ДНФ та вибрати серед них мінімальні форми.
10. Привести булеву функцію  до ДДНФ та мінімізувати її аналітичним методом.
до ДДНФ та мінімізувати її аналітичним методом.
11. За допомогою методу Квайна мінімізувати функцію  .
.
B6
1. Побудувати таблицю істинності для функції  .
.
2. Показати, що  є фіктивною змінною функції
є фіктивною змінною функції  , що задана формулами:
, що задана формулами:
a)  ;
;
b) 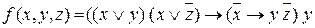 .
.
3. Нехай задана функція  .
.
a) Який порядковий номер цієї функції?
b) Застосовуючи тотожні перетворення, спростити формулу, яка задає  .
.
c) Розкласти функцію  за змінною
за змінною  .
.
d) Побудувати ДКНФ функції  .
.
e) Побудувати  . Чи буде функція
. Чи буде функція  самодвоїстою?
самодвоїстою?
4. Знайти диз’юнктивний розклад функції за змінними  , якщо
, якщо  .
.
5. Нехай задана функція  . За таблицею істинності побудувати ДДНФ і ДКНФ. З’ясувати, чи буде ця функція самодвоїстою.
. За таблицею істинності побудувати ДДНФ і ДКНФ. З’ясувати, чи буде ця функція самодвоїстою.
6. Привести до ДДНФ та ДКНФ функцію  шляхом тотожних перетворень та за допомогою таблиць істинності.
шляхом тотожних перетворень та за допомогою таблиць істинності.
7. З’ясувати, чи будуть повними системи функцій:
a) 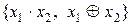 ; b)
; b)  .
.
8. Записати функції, двоїсті до функцій:
a)  ; b)
; b)  .
.
9. З’ясувати, які з елементарних кон’юнкцій, складених з двох змінних, є імплікантами функції  . Чи будуть вказані імпліканти простими?
. Чи будуть вказані імпліканти простими?
10. За допомогою карт Карно мінімізувати булеві функції:
a)  ;
;
b)  .
.
12. За допомогою методу Петрика знайти тупикові ДНФ та вибрати серед них мінімальні форми для булевої функції, яка задана вектором значень  .
.
13. Функція  приймає значення 1 на наборах: 010, 110, 101 та 111. Мінімізувати функцію
приймає значення 1 на наборах: 010, 110, 101 та 111. Мінімізувати функцію  за допомогою методу Квайна.
за допомогою методу Квайна.
C6
1. Знайти фіктивні змінні функції  , що задана вектором значень:
, що задана вектором значень:
a)  ; b)
; b)  .
.
2. Скільки існує різних булевих функцій від  змінних, що зберігають нуль (тобто дорівнюють 0 на нульовому наборі)?
змінних, що зберігають нуль (тобто дорівнюють 0 на нульовому наборі)?
3. Спростити формулу  .
.
4. Довести тотожності:
a)  ;
;
b)  .
.
5. Нехай задана функція  . За таблицею істинності побудувати ДДНФ і ДКНФ. З’ясувати, чи буде ця функція самодвоїстою.
. За таблицею істинності побудувати ДДНФ і ДКНФ. З’ясувати, чи буде ця функція самодвоїстою.
6. Привести булеву функцію  шляхом тотожних перетворень до ДДНФ та ДКНФ.
шляхом тотожних перетворень до ДДНФ та ДКНФ.
7. Знайти всі самодвоїсті функції від двох змінних.
8. Перевірити рівності:
a) 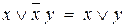 ; b)
; b)  .
.
Записати двоїсті співвідношення та довести їх справедливість.
9. Мінімізувати за допомогою методу Квайна булеву функцію 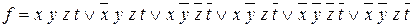 .
.
Графи
 2015-10-22
2015-10-22 9744
9744
