Задача 1. Нехай 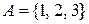 . Вказати властивості відношення
. Вказати властивості відношення 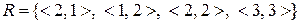 , заданого на множині
, заданого на множині  .
.
Розв’язання. Відношення  не є рефлексивним, оскільки діагональна пара
не є рефлексивним, оскільки діагональна пара 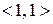 не належить
не належить  . Дане відношення містить діагональні пари
. Дане відношення містить діагональні пари 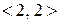 і
і 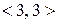 , тому воно не є іррефлексивним. Безпосередньою перевіркою встановлюємо, що з кожною парою виду
, тому воно не є іррефлексивним. Безпосередньою перевіркою встановлюємо, що з кожною парою виду 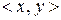 відношення
відношення  містить пару виду
містить пару виду 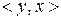 (у нашому випадку до пари
(у нашому випадку до пари 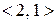 у відношенні є обернена пара
у відношенні є обернена пара 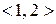 і навпаки; пари
і навпаки; пари 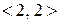 і
і 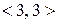 збігаються зі своїми оберненими). Отже, відношення
збігаються зі своїми оберненими). Отже, відношення  є симетричним. Воно не антисиметричне, оскільки
є симетричним. Воно не антисиметричне, оскільки 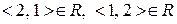 , але
, але 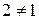 . Відношення
. Відношення  не є транзитивним, оскільки
не є транзитивним, оскільки  містить пари
містить пари 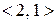 і
і 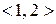 , але не містить пари
, але не містить пари 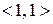 .
.
Задача 2. Класифікувати відношення 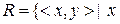 та
та  – особи одного року народження } на множині людей.
– особи одного року народження } на множині людей.
Розв’язання. Відношення  рефлексивне (адже твердження “
рефлексивне (адже твердження “  та
та  – особи одного року народження” істинне для будь-якого
– особи одного року народження” істинне для будь-якого  з множини людей, отже,
з множини людей, отже,  містить усі діагональні пари), симетричне (якщо
містить усі діагональні пари), симетричне (якщо 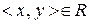 , то це означає, що
, то це означає, що  та
та  – особи одного року народження, але тоді
– особи одного року народження, але тоді  та
та  також є особами одного року народження, звідки
також є особами одного року народження, звідки 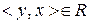 ), транзитивне (якщо
), транзитивне (якщо 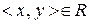 та
та 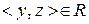 , тобто
, тобто  та
та  – особи одного року народження й
– особи одного року народження й  та
та  – особи одного року народження, то й
– особи одного року народження, то й  та
та  – особи одного року народження, отже,
– особи одного року народження, отже, 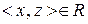 ). Таким чином, дане відношення є відношенням еквівалентності.
). Таким чином, дане відношення є відношенням еквівалентності.
Задача 3. Нехай  ,
, 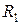 та
та 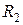 – бінарні відношення на множині
– бінарні відношення на множині  . Довести, що: a)
. Довести, що: a) 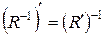 ; b)
; b) 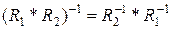 .
.
Розв’язання.
a) Використовуючи означення доповнення відношення та означення відношення, оберненого до даного, маємо: 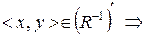
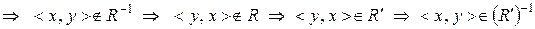 . Отже,
. Отже, 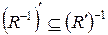 . Покажемо, що
. Покажемо, що 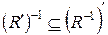 . Маємо:
. Маємо: 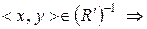
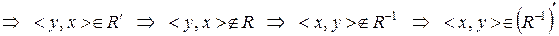 . Це і означає, що
. Це і означає, що 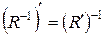 .
.
b) Використовуючи означення відношення, оберненого до даного, та означення добутку відношень, маємо: 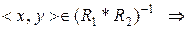
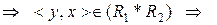 існує такий елемент
існує такий елемент  з множини
з множини  , що
, що 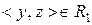 та
та 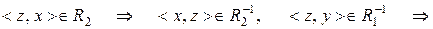
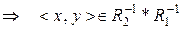 . Отже,
. Отже, 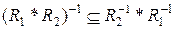 . Покажемо, що
. Покажемо, що 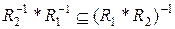 . Маємо:
. Маємо: 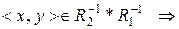
 існує такий елемент
існує такий елемент  з множини
з множини  , що
, що 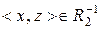 та
та 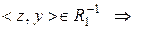
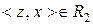 ,
, 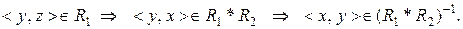 Отже, доведено, що
Отже, доведено, що 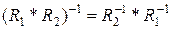 .
. 
Задача 4. Нехай  та
та 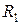 – часткові порядки на
– часткові порядки на  . Довести, що
. Довести, що 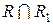 – частковий порядок на
– частковий порядок на  .
.
Розв’язання. Покажемо, що відношення 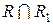 є рефлексивним, антисиметричним та транзитивним. Оскільки
є рефлексивним, антисиметричним та транзитивним. Оскільки  та
та 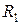 – часткові порядки на
– часткові порядки на  , то відношення
, то відношення  та
та 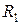 є рефлексивними, тобто і відношення
є рефлексивними, тобто і відношення 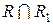 рефлексивне. Нехай
рефлексивне. Нехай  та
та 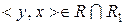 . Тоді
. Тоді 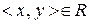 і
і 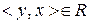 , звідки з антисиметричності
, звідки з антисиметричності  випливає, що
випливає, що 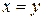 . Отже, відношення
. Отже, відношення 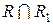 – антисиметричне. Доведемо транзитивність. Нехай
– антисиметричне. Доведемо транзитивність. Нехай  та
та 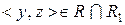 . Тоді
. Тоді 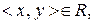
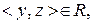
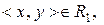
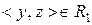 . З транзитивності відношень
. З транзитивності відношень  та
та 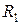 випливає, що
випливає, що 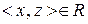 та
та 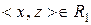 , тобто
, тобто 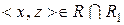 . Таким чином,
. Таким чином, 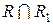 є частковим порядком на
є частковим порядком на  .
.
Задача 5. З’ясувати, чи будуть відношення 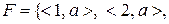
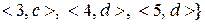 ,
, 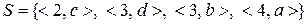 та
та 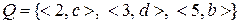 , задані на множинах
, задані на множинах 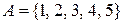 та
та 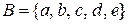 , відображеннями (або частковими відображеннями).
, відображеннями (або частковими відображеннями).
Розв’язання. Відношення  є відображенням множини
є відображенням множини  у
у  , тому що
, тому що  функціональне та його область визначення
функціональне та його область визначення 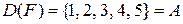 , оскільки
, оскільки 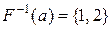 ,
, 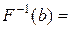 Ø,
Ø, 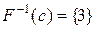 ,
, 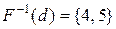 ,
, 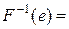 Ø. Відношення
Ø. Відношення 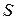 не є відображенням, оскільки воно не є функціональним (елемент 3 з множини
не є відображенням, оскільки воно не є функціональним (елемент 3 з множини  зустрічається двічі, тобто більше одного разу, на першому місці у парах, які належать
зустрічається двічі, тобто більше одного разу, на першому місці у парах, які належать 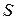 ). Відношення
). Відношення 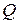 є частковим відображенням
є частковим відображенням  у
у  , тому що
, тому що 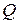 функціональне та його область визначення
функціональне та його область визначення 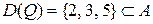 .
.
Задача 6. З’ясувати, чи будуть сюр’єктивними відображення 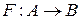 ,
, 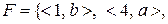
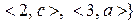 , та
, та 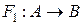 ,
, 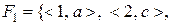
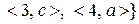 , де
, де 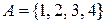 та
та 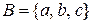 .
.
Розв’язання. Для кожного елемента  з множини
з множини  обчислимо повний прообраз
обчислимо повний прообраз 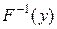 :
: 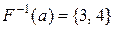 ,
, 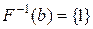 ,
, 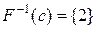 . Таким чином,
. Таким чином, 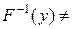 Ø для кожного
Ø для кожного 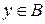 , отже,
, отже,  є сюр’єктивним відображенням (відображенням
є сюр’єктивним відображенням (відображенням  на
на  ). В той же час для відображення
). В той же час для відображення  маємо
маємо 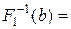 Ø, тому
Ø, тому  не є сюр’єктивним.
не є сюр’єктивним.
Задача 7. З’ясувати, чи будуть ін ’є ктивними відображення 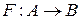 ,
, 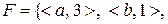
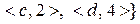 , та
, та 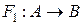 ,
, 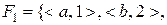
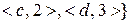 , де
, де 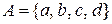 та
та 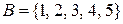 .
.
Розв’язання. Відображення  є ін’єктивним, оскільки різні елементи з області визначення мають різні образи. В той же час у відображенні
є ін’єктивним, оскільки різні елементи з області визначення мають різні образи. В той же час у відображенні  різні елементи
різні елементи  та
та  мають однаковий образ 2, тому
мають однаковий образ 2, тому  не є ін’єктивним.
не є ін’єктивним.
Задача 8. З’ясувати, чи будуть бієктивними (взаємно однозначними) відображення 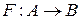 ,
, 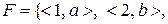
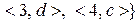 , та
, та 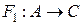 ,
, 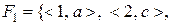
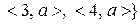 , де
, де 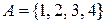 ,
, 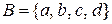 та
та 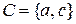 .
.
Розв’язання. Відображення  є сюр’єктивним, оскільки кожен елемент множини
є сюр’єктивним, оскільки кожен елемент множини  має прообраз; крім того, різні елементи множини
має прообраз; крім того, різні елементи множини  мають різні образи, отже,
мають різні образи, отже,  є ін’єктивним. Таким чином,
є ін’єктивним. Таким чином,  є бієкцією. Відображення
є бієкцією. Відображення  не є ін’єктивним, хоча є сюр’єктивним. Отже,
не є ін’єктивним, хоча є сюр’єктивним. Отже,  не є бієктивним.
не є бієктивним.
A3
1. Навести приклади унарних відношень на множині натуральних чисел 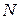 та на множині людей
та на множині людей 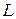 .
.
2. Навести приклад тернарного відношення на множині відрізків.
3. Скільки унарних та тернарних відношень можна побудувати на множині  , якщо вона містить
, якщо вона містить  елементів?
елементів?
4. На множині 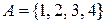 побудувати відношення тотожності
побудувати відношення тотожності  :
: 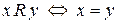 .
.
5. На множині 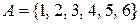 побудувати відношення
побудувати відношення  : “мати спільний дільник, що не дорівнює 1”. Задати це відношення графіком, матрицею та стрілковою діаграмою.
: “мати спільний дільник, що не дорівнює 1”. Задати це відношення графіком, матрицею та стрілковою діаграмою.
6. Нехай 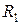 та
та 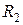 – відношення на множині
– відношення на множині 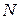 ,
, 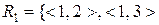 ,
, 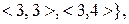
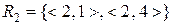 . Знайти
. Знайти 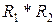 ,
, 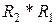 ,
, 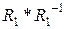 .
.
7. Нехай 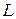 – множина людей,
– множина людей, 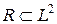 ,
, 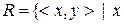 є дитиною
є дитиною 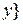 . Яким буде відношення
. Яким буде відношення 
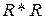 ?
?
8. Відношення 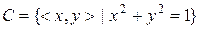 задане на множині дійсних чисел. Побудувати
задане на множині дійсних чисел. Побудувати 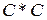 .
.
9. Визначити властивості відношень 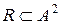 ,
, 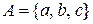 , якщо:
, якщо:
a) 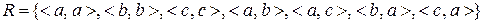 ;
;
b)  .
.
10. Визначити властивості відношень, побудованих чи наведених у задачах № 4, 5, 6, 7.
11. Вказати властивості відношення, заданого на множині людей 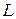 :
: 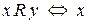 та
та  мають спільного предка.
мають спільного предка.
12. На множині 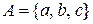 побудувати відношення, яке є
побудувати відношення, яке є
a) рефлексивним, не симетричним, транзитивним;
b) іррефлексивним, не антисиметричним, транзитивним.
13. Класифікувати відношення:
a) 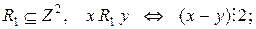
b) 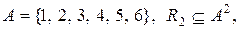
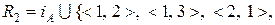
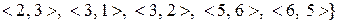 .
.
Для відношень еквівалентності побудувати класи еквівалентності.
14. З’ясувати, чи є наведені відношення відношеннями еквівалентності:
a) “вчитись в одній групі” на множині студентів КПІ;
b) “мати таку ж парність, як …” на множині 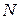 ;
;
c) “мати стільки ж знаків, скільки …” на множині 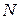 ;
;
d) 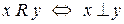 на множині прямих;
на множині прямих;
e) 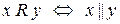 на множині прямих.
на множині прямих.
Для відношень еквівалентності побудувати класи еквівалентності.
15. Відношення еквівалентності на множині 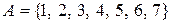 задано розбиттям на класи
задано розбиттям на класи 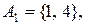
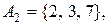
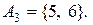 Представити це відношення множиною впорядкованих пар, матрицею та графом.
Представити це відношення множиною впорядкованих пар, матрицею та графом.
16. На множині різнокольорових кульок різного діаметра побудувати відношення еквівалентності.
17. Нехай  – скінченна множина. Які відношення еквівалентності породжують найбільшу та найменшу кількість класів еквівалентності?
– скінченна множина. Які відношення еквівалентності породжують найбільшу та найменшу кількість класів еквівалентності?
18. Класифікувати відношення, 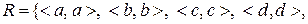
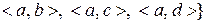 , задане на множині
, задане на множині 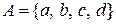 . Побудувати матрицю цього відношення та діаграму Хаасе. Вказати мінімальний, максимальний, найбільший та найменший елементи.
. Побудувати матрицю цього відношення та діаграму Хаасе. Вказати мінімальний, максимальний, найбільший та найменший елементи.
19. На булеані множини 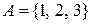 задане відношення
задане відношення 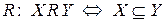 . Побудувати діаграму Хаасе, вказати елементи, які не можна порівняти за цим відношенням. Вказати мінімальний, максимальний, найбільший та найменший елементи.
. Побудувати діаграму Хаасе, вказати елементи, які не можна порівняти за цим відношенням. Вказати мінімальний, максимальний, найбільший та найменший елементи.
20. Скільки різних відношень часткового порядку можна побудувати на трьохелементній множині. Побудувати діаграми Хаасе.
21. Чи може один і той же елемент частково впорядкованої множини бути одночасно мінімальним і максимальним?
22. Якщо впорядкована множина має найменший елемент, то він єдиний. Довести.
23. Класифікувати відношення 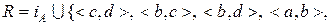
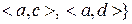 , задане на множині
, задане на множині 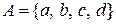 . Побудувати матрицю цього відношення та діаграму Хаасе.
. Побудувати матрицю цього відношення та діаграму Хаасе.
24. З’ясувати тип порядку (частковий, строгий, лінійний):
a) на множині співробітників банку задане відношення “підлеглий – начальник”;
b) на множині офіцерських звань задане відношення “бути молодшим за званням”;
c) на множині деталей задане відношення “бути важчим”.
25. Розташувати у лексикографічному порядку елементи множини:
a) 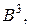 де
де 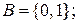 b)
b) 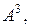 де
де 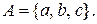
26. Бінарне відношення  є одночасно симетричним і антисиметричним. Довести, що
є одночасно симетричним і антисиметричним. Довести, що  – транзитивне.
– транзитивне.
27. Довести, що об’єднання двох рефлексивних відношень є рефлексивним.
28. Нехай 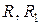 – бінарні відношення, задані на множині
– бінарні відношення, задані на множині  . Довести:
. Довести:
a) 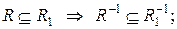
b) 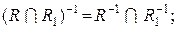
c)  – транзитивне
– транзитивне  .
.
29. Нехай 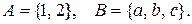 Побудувати приклади відношень
Побудувати приклади відношень 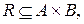 кожне з яких є:
кожне з яких є:
a) повністю визначене на  і не функціональне;
і не функціональне;
b) не повністю визначене на  і не функціональне;
і не функціональне;
c) не повністю визначене на  і функціональне;
і функціональне;
d) повністю визначене на  і функціональне.
і функціональне.
30. Нехай  – відношення між елементами множин
– відношення між елементами множин 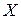 та
та 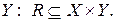 В яких випадках
В яких випадках  можна розглядати як відображення, якщо:
можна розглядати як відображення, якщо:
a) 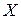 – множина студентів,
– множина студентів, 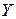 – множина навчальних дисциплін;
– множина навчальних дисциплін; 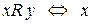 вивчає
вивчає  ;
;
b) 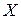 – множина спортсменів,
– множина спортсменів, 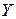 – множина дійсних чисел;
– множина дійсних чисел; 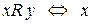 має зріст
має зріст  ;
;
c) 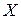 – множина деталей,
– множина деталей, 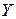 – їх маса;
– їх маса; 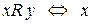 має масу
має масу  ?
?
31. З’ясувати властивості відображення 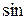 , якщо
, якщо
a) 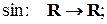 с)
с) 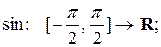
b) 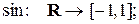 d)
d) 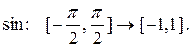
32. Вибрати множини та побудувати на них відображення, яке є:
a) довільним; b) сюр’єктивним, але не ін’єктивним; c) ін’єктивним, але не сюр’єктивним; d) бієктивним; e) тотожним.
33. Чи є рівнопотужними множини:
a) 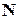 та
та 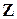 ; с)
; с) 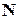 та
та 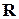 ;
;
b) 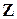 та
та 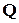 ; d)
; d) 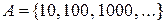 та
та 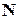 ?
?
34. Множини  і
і  – скінченні. Якщо ці множини еквівалентні, то вони містять однакову кількість елементів. Довести.
– скінченні. Якщо ці множини еквівалентні, то вони містять однакову кількість елементів. Довести.
35. Чи будуть множини  і
і  еквівалентними, якщо
еквівалентними, якщо
a) 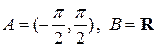 ; b)
; b) 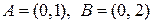 ?
?
36. Чи будуть еквівалентними множини точок на будь-яких двох відрізках 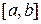 і
і 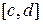 ?
?
37. Нескінченна підмножина зліченної множини зліченна. Довести.
B3
1. На множині студентів 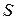 навести приклади повного та порожнього бінарного відношення.
навести приклади повного та порожнього бінарного відношення.
2. На множині 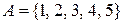 побудувати відношення
побудувати відношення  :
: 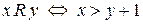 . Задати його різними способами.
. Задати його різними способами.
3. Задати відношення 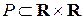 координатним способом:
координатним способом:
a) 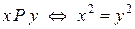 ; b)
; b) 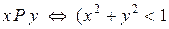 та
та 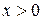 ).
).
4. Нехай на множинах 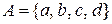 та
та 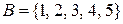 задано відношення
задано відношення 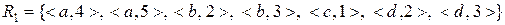 і
і 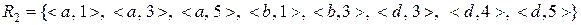 . Побудувати
. Побудувати 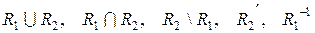 .
.
5. Нехай на множині людей 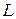 задані такі відношення
задані такі відношення 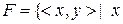 є батьком
є батьком 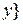 та
та 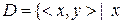 є донькою
є донькою 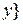 . Описати такі відношення:
. Описати такі відношення:  .
.
6. Відношення  задане на множині
задане на множині  , вказати його властивості, якщо:
, вказати його властивості, якщо:
a) 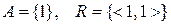 ;
;
b) 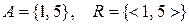 ;
;
c) 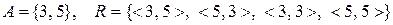 ;
;
d)  ;
;
e) 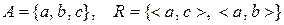 .
.
7. З’ясувати, які властивості мають відношення, задані на множині натуральних чисел:
a) 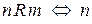 та
та 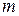 взаємно прості;
взаємно прості;
b) 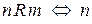 є дільником
є дільником 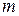 ;
;
c)  ;
;
d) 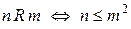 .
.
8. Навести приклад відношень, кожне з яких є
a) рефлексивним, симетричним, не транзитивним;
b) не рефлексивним, не симетричним, транзитивним;
c) рефлексивним, антисиметричним, не транзитивним.
9. Довести, що відношення 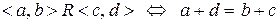 , задане на множині
, задане на множині 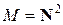 , є відношенням еквівалентності.
, є відношенням еквівалентності.
10. Чи буде відношенням еквівалентності відношення подібності на множині трикутників?
11. Нехай 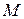 – множина прямих. З’ясувати, чи будуть наступні відношення відношеннями еквівалентності:
– множина прямих. З’ясувати, чи будуть наступні відношення відношеннями еквівалентності:
a) пряма  перетинається з прямою
перетинається з прямою  ;
;
b) пряма  лежить в одній площині з прямою
лежить в одній площині з прямою  ;
;
c) пряма  перетинає ті ж самі площини, що і пряма
перетинає ті ж самі площини, що і пряма  .
.
12. Нехай на множині  задано відношення
задано відношення  . З’ясувати, чи буде
. З’ясувати, чи буде  відношенням еквівалентності, якщо:
відношенням еквівалентності, якщо:
a) 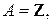
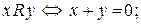
b) 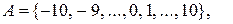
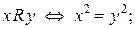
c) 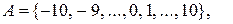
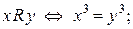
d) 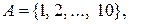
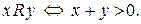
Для кожного відношення еквівалентності побудувати класи еквівалентності..
13. Знайти класи еквівалентності для відношень, заданих на 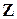 :
:
a) 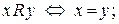 b)
b) 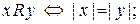 c)
c) 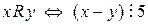 .
.
14. Класифікувати відношення, задані на множині  :
:
a) 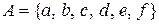 ,
, 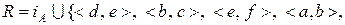
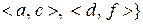 ;
;
b) 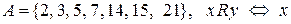 ділить
ділить  .
.
Побудувати матриці відношень та діаграми Хаасе. Вказати мінімальний, максимальний, найбільший та найменший елементи.
15. Нехай 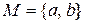 . Скільки відношень часткового порядку можна побудувати на цій множині? Вказати їх.
. Скільки відношень часткового порядку можна побудувати на цій множині? Вказати їх.
16. З’ясувати, чи будуть наведені відношення відношеннями порядку:
a) 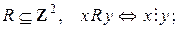
b) 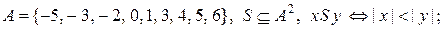
c) 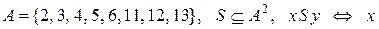 ділиться на
ділиться на  з остачею
з остачею 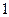 .
.
Вказати тип впорядкованості у випадках, коли це можливо. Побудувати діаграми Хаасе.
17. Опишіть симетричні відношення, які є відношеннями часткового порядку.
18. Довести, що перетин двох симетричних відношень є симетричним.
19. Нехай 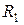 та
та 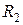 – іррефлексивні відношення. Чи завжди буде добуток таких відношень іррефлексивним? Навести приклади.
– іррефлексивні відношення. Чи завжди буде добуток таких відношень іррефлексивним? Навести приклади.
20. Нехай  ,
, 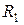 та
та 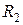 – бінарні відношення, задані на множині
– бінарні відношення, задані на множині  . Довести:
. Довести:
a) 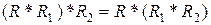 ;
;
b) 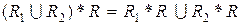 ;
;
c) 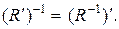
21. Чи кожна підмножина 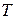 множини
множини 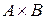 є графіком певного відображення
є графіком певного відображення 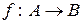 ?
?
22. На множинах 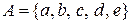 і
і 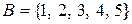 задано відношення:
задано відношення:
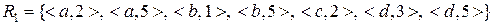 ;
;
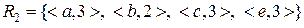 ;
;
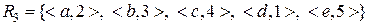 ;
;
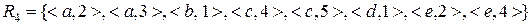 ;
;
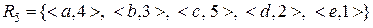 .
.
Які з них: a) всюди визначені; b) функціональні; c) ін’єктивні; d) сюр’єктивні; e) бієктивні (взаємно однозначні)?
23. Чи є відношення
a) 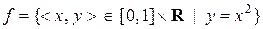 ;
;
b) 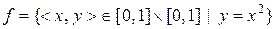 ;
;
c) 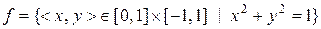 ;
;
d) 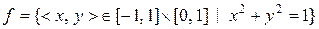 ;
;
e) 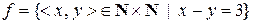 ;
;
f) 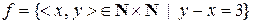 ;
;
g) 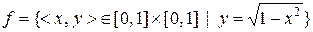 .
.
відображеннями? Вказати їх властивості.
24. Що можна сказати про множини  та
та  , коли відомо, що кожне відображення
, коли відомо, що кожне відображення 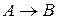 є: а) сюр’єкцією; b) ін’єкцією; c) бієкцією?
є: а) сюр’єкцією; b) ін’єкцією; c) бієкцією?
25. Навести приклад множини 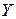 , що еквівалентна множині
, що еквівалентна множині 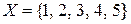 . Скільки взаємно однозначних відображень існує між
. Скільки взаємно однозначних відображень існує між 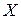 та
та 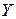 ?
?
26. Чи є зліченною множина 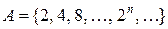 ?
?
27. Чи будуть множини  і
і  еквівалентними, якщо:
еквівалентними, якщо:
a) 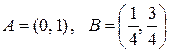 ; b)
; b) 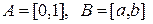 ?
?
28. Довести, що декартів добуток двох зліченних множин є множина зліченна.
29. Чи є зліченною множина 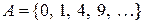 ?
?
С3
1. Множина  складається з
складається з  елементів. Скільки різних бінарних відношень можна побудувати на цій множині? Скільки буде серед них:
елементів. Скільки різних бінарних відношень можна побудувати на цій множині? Скільки буде серед них:
a) рефлексивних відношень; b) симетричних відношень?
2. Визначити, чи будуть вказані відношення відношеннями еквівалентності:
a) 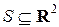 ,
, 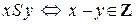 ;
;
b) 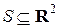 ,
, 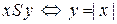 ;
;
c) 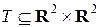 ,
, 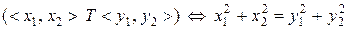 ;
;
d) 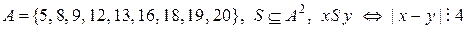 .
.
Для відношень еквівалентності задати класи еквівалентності.
3. Чи можна стверджувати, що об’єднання двох відношень еквівалентності теж буде еквівалентністю? Відповідь обґрунтувати.
4. Побудувати відношення часткового порядку на множині трикутників.
5. Якщо  – відношення часткового порядку, то
– відношення часткового порядку, то 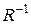 теж відношення часткового порядку. Довести.
теж відношення часткового порядку. Довести.
6. Нехай 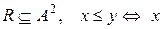 ділиться на
ділиться на  . Вказати мінімальний, максимальний, найменший, найбільший елементи, якщо:
. Вказати мінімальний, максимальний, найменший, найбільший елементи, якщо:
a) 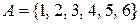 ; b)
; b) 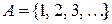 ; c)
; c) 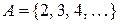 .
.
7. Нехай 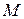 – сукупність непорожніх власних підмножин множини
– сукупність непорожніх власних підмножин множини 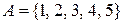 , впорядкована відношенням включення. Вказати мінімальний, максимальний, найменший, найбільший елементи.
, впорядкована відношенням включення. Вказати мінімальний, максимальний, найменший, найбільший елементи.
8. Нехай на множині 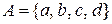 задано відношення
задано відношення 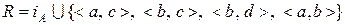 . Знайти лінійний порядок
. Знайти лінійний порядок 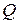 , для якого
, для якого 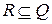 . Скільки існує таких лінійних порядків?
. Скільки існує таких лінійних порядків?
9. Нехай 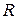 і
і 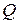 – бінарні відношення, задані на множині
– бінарні відношення, задані на множині  . Довести:
. Довести:
а) 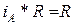 ; b)
; b) 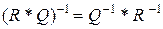 .
.
10. Довести, що  – симетричне відношення тоді і тільки тоді, коли
– симетричне відношення тоді і тільки тоді, коли 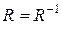 .
.
11. Довести, що  – антисиметричне відношення тоді і тільки тоді, коли
– антисиметричне відношення тоді і тільки тоді, коли 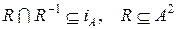 .
.
12. Якщо  – відношення еквівалентності, то
– відношення еквівалентності, то 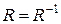 та
та 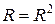 . Довести.
. Довести.
13. Нехай 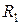 та
та 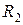 – відношення еквівалентності. Довести, що
– відношення еквівалентності. Довести, що 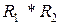 – відношення еквівалентності тоді і тільки тоді, коли
– відношення еквівалентності тоді і тільки тоді, коли 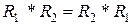 .
.
14. Нехай 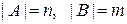 . Скільки можна побудувати різних відображень
. Скільки можна побудувати різних відображень 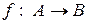 ?
?
15. Нехай 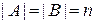 . Скільки можна побудувати різних бієкцій
. Скільки можна побудувати різних бієкцій 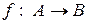 ?
?
16. На множинах  та
та  задано відношення
задано відношення  . За яких умов відношення
. За яких умов відношення 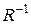 є: a) всюди визначеним; b) функціональним; c) ін’єктивним; d) сюр’єктивним; e) бієктивним?
є: a) всюди визначеним; b) функціональним; c) ін’єктивним; d) сюр’єктивним; e) бієктивним?
 2015-10-22
2015-10-22 7013
7013
