1. Скорость u света в среде

где с – скорость света в вакууме; n – показатель преломления среды.
2. Оптическая длина пути световой волны

где  – геометрическая длина пути световой волны в среде с показателем преломления n.
– геометрическая длина пути световой волны в среде с показателем преломления n.
3. Оптическая разность хода двух световых волн

4. Зависимость разности фаз от оптической разности хода световых волн

где  – длина световой волны в вакууме.
– длина световой волны в вакууме.
5. Условие максимального усиления света при интерференции

6. Условие максимального ослабления света при интерференции

7. Оптическая разность хода световых волн, возникающих при отражении монохроматического света от тонкой плёнки, находящейся в вакууме или воздухе
 или
или 
где d – толщина плёнки; n – показатель преломления;  – угол падения;
– угол падения;
 – угол преломления света в плёнке.
– угол преломления света в плёнке.
В оптическую разность хода добавляют  , так как при отражении световой волны от оптически более плотной среды фаза колебаний вектора напряжённости электрического поля
, так как при отражении световой волны от оптически более плотной среды фаза колебаний вектора напряжённости электрического поля 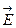 в волне (светового вектора) меняется на p.
в волне (светового вектора) меняется на p.
8. Условие дифракционных максимумов от одной щели

где a – ширина щели;  – угол дифракции; k – порядковый номер максимума.
– угол дифракции; k – порядковый номер максимума.
9. Условие дифракционных минимумов от одной щели

10. Условие для главных максимумов на дифракционной решётке

где d – период дифракционной решётки;  – угол между нормалью к поверхности решётки и направлением на данный максимум;
– угол между нормалью к поверхности решётки и направлением на данный максимум;
k – порядковый номер главного максимума.
11. Энергия кванта электромагнитного излучения

12. Уравнение Эйнштейна для внешнего фотоэффекта

где  – энергия фотона, падающего на поверхность металла; А – работа выхода электрона из металла;
– энергия фотона, падающего на поверхность металла; А – работа выхода электрона из металла; 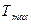 – максимальная кинетическая энергия электрона.
– максимальная кинетическая энергия электрона.
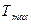 в нерелятивистском и релятивистском случаях выражается разными формулами:
в нерелятивистском и релятивистском случаях выражается разными формулами:
1) если энергия фотона  , то электрон классический и кинетическая энергия электрона равна:
, то электрон классический и кинетическая энергия электрона равна:

где  – масса покоя электрона;
– масса покоя электрона;  – задерживающее напряжение),
– задерживающее напряжение),  МэВ – энергия покоя электрона;
МэВ – энергия покоя электрона;
2) если  , то электрон релятивистский и кинетическая энергия электрона равна:
, то электрон релятивистский и кинетическая энергия электрона равна:

где m – масса релятивистского электрона.
“Красная граница” фотоэффекта для данного металла
 или
или 
где  – максимальная длина волны излучения (
– максимальная длина волны излучения (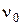 – соответственно минимальная частота), при которой фотоэффект ещё возможен.
– соответственно минимальная частота), при которой фотоэффект ещё возможен.
13. Энергия, масса и импульс фотона
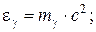
 ;
; 
Пример 10. На дифракционную решётку длиной 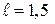 мм, содержащей N = 300 штрихов, падает нормально монохроматический свет с длиной волны
мм, содержащей N = 300 штрихов, падает нормально монохроматический свет с длиной волны 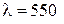 нм. Определить:
нм. Определить:
1) число максимумов, наблюдаемых в спектре дифракционной решётки;
2) угол, соответствующий последнему максимуму.
Дано: 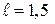 мм =
мм =  м; N = 300;
м; N = 300; 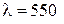 нм =
нм =  м.
м.
Найти: 1) N; 2) 
Решение: Согласно условиюзадачи изобразим рисунок (рис. 10):

Рис.10
На рисунке изображён график зависимости интенсивности света на экране от расстояния x (I = f (x)).
1) Период дифракционной решётки определим по формуле

Подставляя числовые данные, получим:
 м =5 мкм.
м =5 мкм.
Условие главных максимумов на дифракционной решётке
 (1)
(1)
Поскольку наибольший угол отклонения лучей решёткой не может быть более  , из условия (1) можно найти максимальное значение
, из условия (1) можно найти максимальное значение  , при
, при  :
:
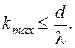
Подставляя данные, получим:
 .
.
Число k должно быть обязательно целым. В то же время оно не может быть равным 10, так как при этом значении  будет больше единицы, что невозможно.
будет больше единицы, что невозможно.
Общее число максимумов, даваемое дифракционной решёткой

так как максимумы наблюдаются как справа, так и слева от центрального максимума (единица учитывает центральный нулевой максимум).
Вычисляя, получим:

2)Угол дифракции, соответствующий последнему максимуму, найдём, записав условие (1) в виде:

Откуда

Выполним вычисления:

Ответ: 1) N = 19; 2)  .
.
Пример 11. Определить “красную границу” фотоэффекта для цезия, если при облучении его поверхности фиолетовыми лучами длиной волны 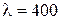 нм максимальная скорость фотоэлектронов
нм максимальная скорость фотоэлектронов  м/с.
м/с.
Дано: 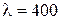 нм =
нм = 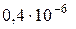 м;
м;  м/с.
м/с.
Найти: 
Решение: “Красной границей” фотоэффекта называется наибольшая длина волны  облучающего света, при которой ещё возможен фотоэффект с поверхности данного металла.
облучающего света, при которой ещё возможен фотоэффект с поверхности данного металла.
При облучении светом этой длины волны скорость, а следовательно, и кинетическая энергия электронов равны нулю. Поэтому уравнение Эйнштейна для фотоэффекта
 (1)
(1)
в случае “красной границы” запишется в виде:
 или
или 
Отсюда  (2)
(2)
Работу выхода для цезия определим с помощью уравнения (1)
 (3)
(3)
Подставляя числовые данные в (3), вычислим работу выхода:
 Дж.
Дж.
Тогда
 м.
м.
Ответ: 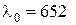 нм.
нм.
ЭЛЕ М ЕНТЫ АТОМНОЙ И ЯДЕРНОЙ ФИЗИКИ
 2015-10-22
2015-10-22 443
443








