2015-10-22
4311
Двойной интеграл введем аналогично определению геометрического смысла определенного интеграла функции одного переменного: если функция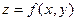 
непрерывна и неотрицательна в области 
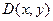, то двойным интегралом 
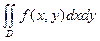называется объем прямого цилиндрического тела (цилиндроида – см. рисунок), построенного на области 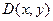как на основании и ограниченного сверху поверхностью .
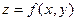Заметим, что неопределенные двойные интегралы на практике не встречаются, поэтому не будем обсуждать непростое понятие первообразной, которая должна учитывать частные производные. Свойства же двойного интеграла те же, что и у однократного.
Интегрирование функции двух переменных значительно более трудная и арифметически громоздкая задача по сравнению с задачей для одной переменной. Рассмотрим наиболее распространенную на практике методику вычисления двойного интеграла сведением к повторному интегрированию.
 |
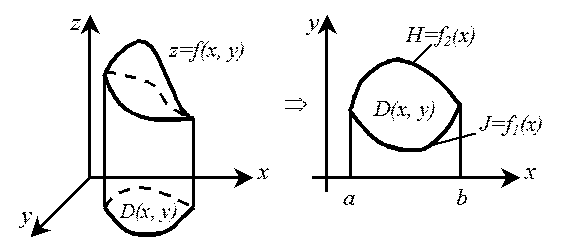В этой методике ключевым моментом является область интегрирования
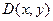. Если эта область непрерывна (см. рисунок) и ее границы могут быть четко определены, то для непрерывной в этой области функции 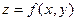справедлива формула 
.
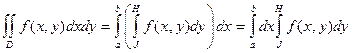Таким образом, двойной интеграл сводится к последовательному вычислению двух однократных определенных интегралов ( повторных интегралов ). При этом внутренний интеграл имеет функциональные (или числовые) пределы интегрирования, а внешний – всегда числовые. Внутренний интеграл (по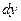 
) вычисляется в предположении, что х – постоянная величина (полная аналогия с вычислением частных производных). Расчет производится с помощью двукратного применения обычной формулы Ньютона – Лейбница.
Заметим, что область интегрирования 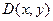может быть и бесконечной в одном или в обоих направлениях осей координат. Тогда, при непрерывности функции 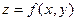, имеем несобственные двойные интегралы первого рода, которые, очевидно, сводятся к несобственным повторным интегралам.
Наиболее простым будет случай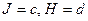 
, где с и d – константы, т.е. прямоугольник 
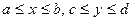. Тогда
.
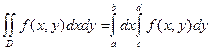Для практического вычисления двойного интеграла рекомендуется следующая схема:
1. Сделать эскиз области интегрирования 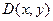, определить все функциональные и числовые границы;
2. С помощью формулы Ньютона – Лейбница вычислить внутренний интеграл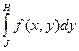 
(или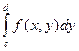 
- для прямоугольника). Ответом, как правило, будет некоторая функция одного аргумента 
;
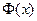3. С помощью формулы Ньютона – Лейбница вычислить внешний интеграл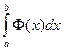 
.
Если область интегрирования 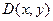имеет сложное очертание, то рекомендуется разбить ее на сумму простых подобластей, например, 
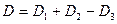. Тогда искомый интеграл будет алгебраической суммой интегралов по подобластям, т.е.
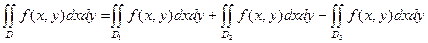
В заключение отметим, что двойной интеграл часто используется для вычисления площади плоских фигур. Формула для вычисления площади имеет вид
.
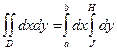Литература
1. Баврин И.И. Высшая математика: учебник для вузов. М.: Владос, 2003.
2. Бугров Я.С. Высшая математика: учебник для вузов. – М.: Дрофа,2003.
3. Виленкин И.В. Высшая математика для студентов экономических, технических, естественно - научных специальностей вузов: учебник для вузов. – Ростов – на Дону: Феникс, 2004.
4. Выгодский М.Я. Справочник по высшей математике. М.: Астрель: АСТ, 2005.
5. Высшая математика для экономистов. Под ред. Кремера Н.Ш. –М.: ЮНИТИ, 2002.
6. Ильин В.А. Высшая математика: учебник для вузов. М.: Проспект, 2005.
- Шипачев В.С. Высшая математика: учебник для ВУЗов. – М..: Высшая школа, 2005.
