ІІІ. Аналітична геометрія

3.1. Аналітична геометрія це розділ математики, в якому геометричні задачі розв’язуються алгебраїчним шляхом за допомогою методу координат.

В аналітичній геометрії геометричні місця точок або лінії задаються рівняннями, що зв’язують в даній системі координат змінн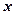і і , які називаються ще поточними координатами. Якщо в елементарній геометрії лінії та їх властивості вивчались в основному за допомогою геометричних побудов, то в аналітичній геометрії вони вивчаються шляхом дослідження рівнянь цих ліній.

Означення. Рівнянням лінії в аналітичній геометрії називається співвідношення, (або залежність між змінними 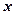і ) вигляду , яке задовольняють координати довільної точки 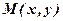цієї лінії, а якщо точка 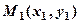не лежить на цій лінії, то її координати не задовольняють дане рівняння.

Наприклад.

1. Координати точки задовольняють рівняння прямої , отже, ця точка лежить на прямій. Координати точки дане рівняння не задовольняють: . Отже, не лежить на даній прямій.

2. Точка лежить на колі , оскільки , а точка не лежить на цьому колі, бо .