2015-10-22
414
Вычисления по этому методу осуществляются в два этапа. На первом этапе по схеме Эйлера находится промежуточное значение 
 .
| (5.5) |
На втором этапе находится значение yi+1 по схеме
 ,
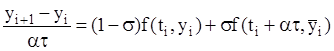| (5.6) |
где a>0, s>0 - параметры. Подставляя 
из (5.5) в (5.6), имеем
 .
| (5.7) |
Нетрудно проверить (разложение по формуле Тейлора), что схема (5.7) имеет второй порядок аппроксимации при условии sa=1/2. Частные случаи разностной схемы (5.7)
 .
| (5.8) |
Эта разностная схема носит название предиктор-корректор, или счет-пересчет. Первая схема из (5.8) - схема Эйлера с шагом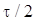 
(предиктор), вторая - схема со значением на полушаге (корректор)
