Задачу вычисления расстояния от точки до прямой можно решить, используя уже полученные знания.
Пусть дана точка М(-1;1) и прямая m: 3х-4у+12=0. (Рис). Найти расстояние от точки М до прямой m. Расстояние от точки до прямой равно длине перпендикуляра MN, опущенного из точки М на прямую m В таком случае необходимо:
1. Записать уравнение прямой MN, проходящей через точку М перпендикулярно m. (Это будет прямая 4х+3у+1=0. Убедитесь в этом.)
2. Найти координаты точки пересечения прямых MN и m. Для этого необходимо решить систему уравнений
 . (Имеем для точки N координаты
. (Имеем для точки N координаты  . Найдите их.)
. Найдите их.)
3. Найти расстояние между точками М и N.(Расстояние между точками М и N
|MN|=1. Вычислите и убедитесь)
Эту же задачу можно решить, используя формулу вычисления расстояния d от точки М0(х0; у0) до прямой Ах+Ву+С=0, которая имеет вид:  . Для нашей задачи мы получим:
. Для нашей задачи мы получим:  .
.
Задача 1 Составить уравнение прямой, проходящей через точку (1,3) перпендикулярно прямой 
1 способ. Разрешив уравнение прямой относительно y 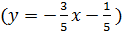 ,
,
находим  . Используя условие перпендикулярности прямых (
. Используя условие перпендикулярности прямых (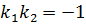 ), находим
), находим  . Искомое уравнение:
. Искомое уравнение:  . Окончательно получаем:
. Окончательно получаем: 
2 способ. Используя условие перпендикулярности прямых
( ), уравнение можно записать в виде:
), уравнение можно записать в виде:  . Подставляя координаты данной точки, найдём значение С:
. Подставляя координаты данной точки, найдём значение С:
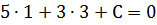 .
.  . Отсюда искомое уравнение:
. Отсюда искомое уравнение: 
3 способ. Уравнение прямой, проходящей через данную точку перпендикулярно прямой  имеет вид:
имеет вид:
 . Поэтому имеем:
. Поэтому имеем:  .
.
Получаем искомое уравнение: 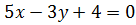
4 способ. Вектор  перпендикулярен прямой
перпендикулярен прямой  .
.
Следовательно, для искомой он является направляющим. Воспользуемся каноническим уравнением: 

 .
.
Задача 2 Составить уравнение биссектрисы углов между прямыми:

 .
.
1 способ. 

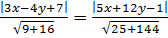





 .
.
2 способ 


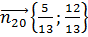 .
.
 +
+ 

 .
.
















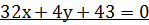
 2015-10-22
2015-10-22 491
491







