Уравнение вида
Ах+Ву+C=0 (А2 +В2  0) (5)
0) (5)
называется общим уравнением прямой на плоскости Оху.
Геометрический смысл коэффициентов 
Взаимное расположение двух прямых на плоскости. Угол между прямыми.
Две прямые на плоскости могут: пересекаться, совпадать либо быть параллельными. Рассмотрим случай, когда прямые пересекаются. 
Рис.2
Пусть прямые заданы уравнениями: у=к1х+в1 и у=к2 х+в2.
Очевидно, что угол между прямыми определяется не однозначно (с точностью до слагаемого, кратного 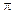 ). Значение угла всегда можно выбрать так, чтобы оно было неотрицательно и меньше
). Значение угла всегда можно выбрать так, чтобы оно было неотрицательно и меньше 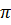 . Обозначим углы наклона прямых к оси Ох соответственно через
. Обозначим углы наклона прямых к оси Ох соответственно через  1 и
1 и  2, а угол между прямыми -
2, а угол между прямыми -  . Тогда
. Тогда  2=
2=  1+
1+  , откуда
, откуда  =
=  2-
2-  1 и
1 и
tg  =tg(
=tg( 2-
2-  1)=
1)=  . Т.к. tg
. Т.к. tg  1= к1 и. tg
1= к1 и. tg  2= к2, получим:
2= к2, получим:



Замечание. Порядок, в котором рассматриваются прямые, можно выбирать произвольно. Он может повлиять на знак тангенса угла. Но т.к. мы выбираем острый угол, то и значение тангенса необходимо брать только положительное. Поэтому в окончательной формуле необходимо ввести знак модуля:
 . ()
. ()
Мы получили формулу для вычисления угла между двумя прямыми.
Если прямые параллельны, то угол  = 0, а значит и tg
= 0, а значит и tg  =0 и, следовательно, k1= k2.
=0 и, следовательно, k1= k2.
Итак, Для параллельности двух прямых необходимо и достаточно, чтобы их угловые коэффициенты были равны.
Пусть прямые перпендикулярны, тогда можно считать, что  2-
2-  1=
1=  . Отсюда
. Отсюда  2=
2=  1+
1+  . И tg
. И tg  =tg (
=tg ( 1+
1+  )=ctg
)=ctg  1=
1=  или
или
tg  1 tg
1 tg  2=-1.
2=-1.
Получаем условие перпендикулярности двух прямых: k1 k2=-1.

С другой стороны угол  между двумя прямыми L1 и L2 -это наименьший из углов между их направляющими векторами
между двумя прямыми L1 и L2 -это наименьший из углов между их направляющими векторами 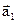 и
и  (Рис. 3).
(Рис. 3).

Обозначим координаты направляющих векторов 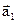 и
и  соответственно (l1, m1) и (l2,m2). Условием параллельности прямых L1 и L2 с направляющими векторами
соответственно (l1, m1) и (l2,m2). Условием параллельности прямых L1 и L2 с направляющими векторами 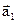 и
и  является условие коллинеарности направляющих векторов (
является условие коллинеарности направляющих векторов ( ), а условием перпендикулярности прямых - условие ортогональности направляющих векторов (
), а условием перпендикулярности прямых - условие ортогональности направляющих векторов ( ). Переходя к координатам направляющих векторов прямых, заданных общими уравнениями
). Переходя к координатам направляющих векторов прямых, заданных общими уравнениями 
чтобы коэффициенты при переменных были пропорциональны
, получим
Условие параллельности двух прямых

 2015-10-22
2015-10-22 2961
2961








