Оценка параметров нелинейных моделей

Нелинейные уравнения регрессии можно разделить на два класса:

– уравнения, которые с помощью замены переменных можно привести к линейному виду в новых переменных x', y'

y¢ = a¢ + b¢× x¢; (3)

– уравнения, для которых это невозможно. Назовем их внутренне нелинейными.

В первом случае уравнения регрессии преобразуются к линейному виду с помощью введения новых (линеаризующих) переменных x', y'. При этом предварительно формируются массивы значений {(x'_i, y'_i), i = 1, …, n }. В последующем, после определения параметров линейного уравнения регрессии с помощью обратного преобразования можно получить параметры исходного уравнения регрессии, представляющие интерес для исследователя.

Линеаризующие преобразования для некоторых нелинейных моделей приведены в таблице 1.

Таблица 1. Линеаризующие преобразования

Зависимость	Формула	Преобразование	Зависимость между параметрами
Гиперболическая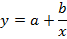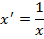
Логарифмическая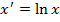
Степенная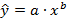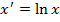
Экспоненциальная
Показательная

Для оценки параметров внутренне нелинейных зависимостей также можно применить метод наименьших квадратов и определять оптимальные значения параметров а и b исходя из условия

. (4)

или

(5)

Но в данном случае условия

(6)

уже не являются линейными алгебраическими уравнениями относительно параметров а и b, поэтому величины параметров а и b удобнее определять непосредственно из условия (5) как значения, доставляющие минимум величине S. Итерационную процедуру минимизации S в общем виде можно представить в виде следующих последовательных шагов.

1. Задаются некоторые «правдоподобные» начальные (исходные) значения а ⁰ и b ⁰ параметров а и b.

2. Вычисляются теоретические значения 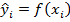с использованием этих значений параметров.

3. Вычисляются остатки 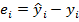и сумма квадратов остатков .

4. Вносятся изменения в одну или более оценку параметров.

5. Вычисляются новые теоретические значения , остатки е_i и S.

6. Если произошло уменьшение S, то новые значения оценок используются в качестве новой отправной точки.

7. Шаги 4, 5 и 6 повторяются до тех пор, пока не будет достигнута ситуация, когда величину S невозможно будет улучшить (в пределах заданной точности).

8. Полученные на последнем шаге значения параметров а и b являются оценками параметров уравнения регрессии, полученными по нелинейным методом наименьших квадратов.

Конкретные методы минимизации S отличаются способом выбора новых измененных значений оценок параметров.

Для примера моделей, которых можно свести к линейной форме, рассмотрим показательную функцию вида:

где случайная ошибка ε_i мультипликативно связана с факторным признаком x_i. Эта модель является нелинейной по параметру β₁. Для ее линеаризации применим вначале процесс логарифмирования:

После логарифмирования воспользуемся методом замен.

Пусть ln y_i = Y_i; ln β₀ = Α; ln β₁ = Β; ln ε_i = Ε.

Преобразованный вид показательной функции можно записать следующим образом:

Показательная функция является внутренне линейной, и оценки ее параметров могут быть найдены с помощью классического метода наименьших квадратов. Однако если взять показательную функцию, включающую случайную ошибку ε_i аддитивно, т. е.

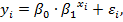
то данную модель уже невозможно привести к линейному виду процессом логарифмирования. Она является внутренне нелинейной. Таким же образом можно рассмотреть и степенную функцию, которая является очень популярной в эконометрических исследованиях.

Степенными функциями являются кривые Энгеля, кривые спроса и предложения, производственные функции.

Пусть задана степенная функция вида:

Заменим следующие показатели в полученном уравнении: ln y_i = Y_i; ln β₀ = Α; ln x_i = X_i; ln ε_i = Ε. Тогда преобразованный вид степенной функции можно записать как:

Степенная функция также является внутренне линейной, и ее оценки можно найти с помощью классического метода наименьших квадратов. Но если взять ее в виде уравнения