Лекция 19. Функция. Область определения и множество значений функции

Функция — одно из важнейших математических понятий.

Определение: Если каждому числу из некоторого множества x поставлено в соответствие единственное число y, то говорят, что на этом множестве задана функция y(x). При этом x называют независимой переменной или аргументом, а y — зависимой переменной или значением функции или простофункцией.

Говорят также, что переменная y является функцией от переменной x.

Обозначив соответствие некоторой буквой, например f, удобно писать: y=f (x), то есть, значение y получается из аргумента x с помощью соответствия f. (Читают: y равно f от x.) Символом f (x) обозначают значение функции, соответствующее значению аргумента, равному x.

Пример 1 Пусть функция задается формулой y=2x²–6. Тогда можно записать, что f(x)=2x²–6. Найдем значения функции для значений х, равных, например, 1; 2,5;–3; т. е. найдем f(1), f(2,5), f(–3):

f(1)=2•1²–6=–4;
f(2,5)=2•2,5²–6=6,5;
f(–3)=2•(–3)²–6= 12.

Заметим, что в записи вида y=f (x) вместо f употребляют и другие буквы: g, и т. п.

Определение: Область определения функции — это все значения x, при которых существует функция.

Если функция задана формулой и ее область определения не указана, то считают, что область определения функции состоит из всех значений аргумента, при которых формула имеет смысл.

Другими словами, область определения функции, заданной формулой, является все значения аргумента, за исключением тех, которые приводят к действиям, которые мы не можем выполнить. На данный момент мы знаем только два таких действия. Мы не можем делить на нуль и не можем извлечь квадратный корень из отрицательного числа.

Определение: Все значения, которые принимает зависимая переменная образуют область значения функции.

Область определения функции, описывающей реальный процесс, зависит от конкретных условий его протекания. Например, зависимость длины l железного стержня от температуры нагревания t выражается формулой, где l₀ начальная длина стержня, а —коэффициент линейного расширения. Указанная формула имеет смысл при любых значениях t. Однако, областью определения функцииl=g(t) является промежуток в несколько десятков градусов, для которого справедлив закон линейного расширения.

Пример.

Укажите область значений функции y = arcsinx.

Решение.

Областью определения арксинуса является отрезок [-1; 1]. Найдем наибольшее и наименьшее значение функции на этом отрезке.

Производная положительна для всех x из интервала (-1; 1), то есть, функция арксинуса возрастает на всей области определения. Следовательно, наименьшее значение она принимает при x = -1, а наибольшее при x = 1.

Мы получили область значений функции арксинуса .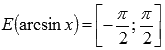

Найдите множество значений функции 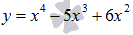на отрезке [1; 4].

Решение.

Найдем наибольшее и наименьшее значение функции на данном отрезке.

Определим точки экстремума, принадлежащие отрезку [1; 4]:

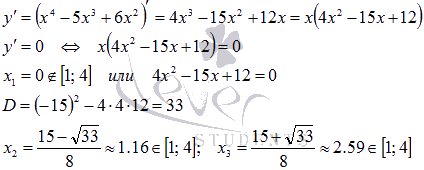
Вычисляем значения исходной функции на концах отрезка и в точках :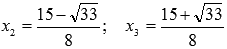

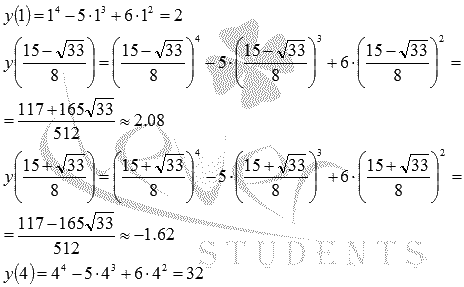
Следовательно, множеством значений функции на отрезке является интервал .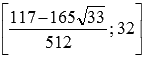

Сейчас покажем, как находить множество значений непрерывной функции y = f(x) на открытых интервалах (a; b), .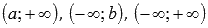

Сначала определяем точки экстремума, экстремумы функции, промежутки возрастания и убывания функции на данном интервале. Далее вычисляем односторонние пределы на концах интервала и (или) пределы на бесконечности (то есть, исследуем поведение функции на границах открытого интервала или на бесконечности). Этой информации достаточно, чтобы найти множество значений функции на таких промежутках.