Формула Ньютона-Лейбница

Пусть 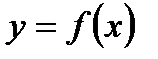непрерывна на 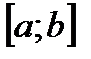и переменная 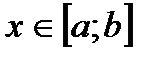. Тогда совокупность всех первообразных для этой функции можно выразить формулой . Легко видеть, что . Откуда, заменив переменную интегрирования снова на х, получим формулу Ньютона –Лейбница:

Для того чтобы вычислить определенный интеграл, прежде всего вычисляется одна из первообразных F(x), затем вычисляется значение этой функции в точке b и вычитается её значение в точке а.

Пример.

Вычислить

.