Рассмотрим функцию 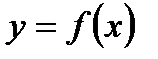 определенную и непрерывную на некотором отрезке
определенную и непрерывную на некотором отрезке 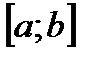 числовой прямой. Разобьем
числовой прямой. Разобьем 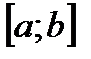 на n отрезков
на n отрезков 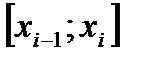 длины
длины 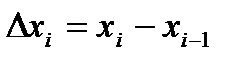 точками
точками 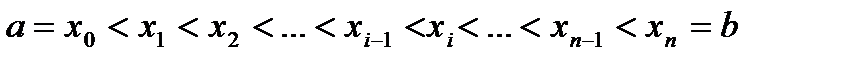 . На каждом i- том отрезке берем произвольную точку
. На каждом i- том отрезке берем произвольную точку 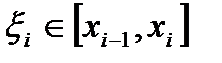 . Вычисляем значение функции
. Вычисляем значение функции 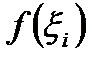 в каждой из этих точек и умножаем его на длину соответствующего отрезка
в каждой из этих точек и умножаем его на длину соответствующего отрезка 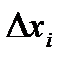 . После чего суммируем по всем отрезкам
. После чего суммируем по всем отрезкам 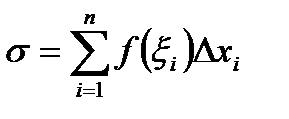 .
.
Полученное выражение называют интегральной суммой. Понятие интегральной суммы играет определяющую роль в определении всех интегралов.
Если предел интегральной суммы при стремлении к нулю максимальной длины 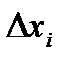 не зависит ни от способа разбиения отрезка
не зависит ни от способа разбиения отрезка 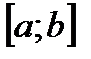 на промежутки
на промежутки 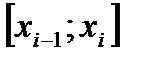 , ни от способа выбора точек
, ни от способа выбора точек 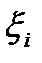 в каждом из этих промежутков, то он называется определенным интегралом от функции
в каждом из этих промежутков, то он называется определенным интегралом от функции 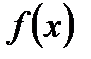 в пределах от а до b и обозначается:
в пределах от а до b и обозначается: 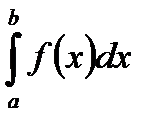 .
.
Свойства определенного интеграла.
I. 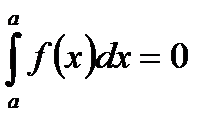
II. 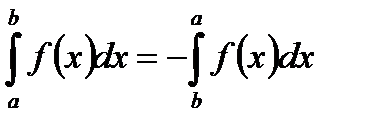
III. 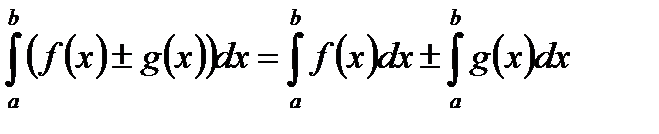
IV. 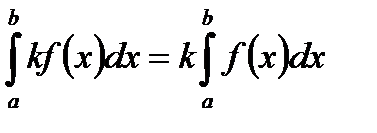
V. 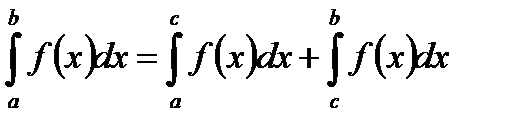
VI. Если 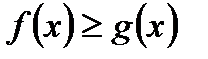 для всех
для всех 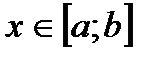 , то
, то 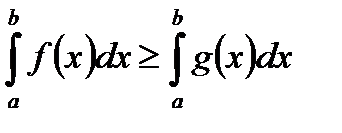
VII. 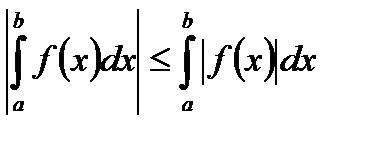 , если a<b.
, если a<b.
VIII. Теорема о среднем. Если f(x) непрерывна на 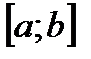 , то существует точка
, то существует точка 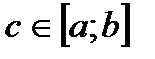 , такая что
, такая что 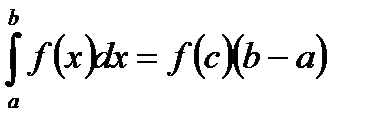
 2015-10-22
2015-10-22 302
302







