(только для студентов заочной формы, со сроком обучения 5 лет)
Вариант 1
Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:.
а)  , б)
, б)  , в)
, в) 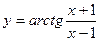 .
.
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Записать уравнение касательной и нормали к графику функции  , в точке, где касательная параллельна прямой
, в точке, где касательная параллельна прямой  . Сделать чертёж.
. Сделать чертёж.
Задание №5. Провести полное исследование функции 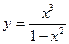 и построить её график.
и построить её график.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а)  , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б)  .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

 .
.
Вариант 2

Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в)  .
.
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Составить уравнения касательных к кривой  , перпендикулярных прямой, проходящей через точки (0;-1) и (-1;4). Сделать чертёж.
, перпендикулярных прямой, проходящей через точки (0;-1) и (-1;4). Сделать чертёж.
Задание №5. Провести полное исследование функции  и построить её график.
и построить её график.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а)  , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б) 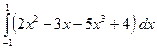 .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

 .
.
Вариант 3
Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а) 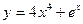 , б)
, б)  , в)
, в)  .
.
Задание №3 Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4.
Пользуясь понятием дифференциала, найти приближённое значение  .
.
Задание №5. Провести полное исследование функции и построить её график: 
 .
.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а)  , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а) 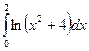 , б)
, б)  .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.



Вариант 4
Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а) 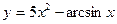 , б)
, б)  , в)
, в) 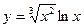 .
.
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Выяснить, в каких точках касательные к графику функции  образуют с осью Ох угол 135
образуют с осью Ох угол 135  . Составить уравнение этих касательных. Сделать чертёж.
. Составить уравнение этих касательных. Сделать чертёж.
Задание №5. Провести полное исследование функции и построить её график:

 .
.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а)  , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б) 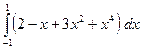 .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

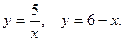


Вариант 5

Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Составить уравнение касательной к кривой  , которая перпендикулярна прямой
, которая перпендикулярна прямой 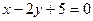 . Сделать чертёж.
. Сделать чертёж.
Задание №5 Провести полное исследование функции и построить её график:

 .
.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а) 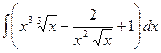 , б)
, б)  , в)
, в) 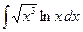 .
.
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б)  .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

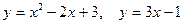 .
.
Вариант 6

Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Записать уравнение касательной и нормали к графику функции  , в точке, где касательная параллельна прямой
, в точке, где касательная параллельна прямой  . Сделать чертёж.
. Сделать чертёж.
Задание №5. Провести полное исследование функции и построить её график:

 .
.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а) 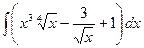 , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а) 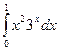 , б)
, б) 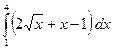 .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.


Вариант 7
Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
а)  , б)
, б)  , в)
, в) 
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Пользуясь понятием дифференциала, найти приближённое значение  .
.
Задание №5. Провести полное исследование функции 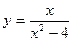 и построить её график.
и построить её график.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а)  , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б)  .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

Вариант 8
Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Составить уравнения касательных к кривым  и
и  в точках их пересечения. Доказать, что касательные перпендикулярны. Сделать
в точках их пересечения. Доказать, что касательные перпендикулярны. Сделать
чертёж.
Задание №5. Провести полное исследование функции и построить её график:

 .
.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а)  , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б)  .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

 .
.
Вариант 9
Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а) 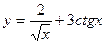 , б)
, б) 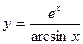 , в)
, в) 
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Пользуясь понятием дифференциала, найти приближённое значение 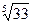 .
.
Задание №5. Провести полное исследование функции и построить её график:

 .
.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а) 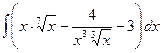 , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б)  .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.
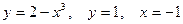 .
.
Вариант 10
Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Записать уравнение касательной и нормали к графику функции  , в точке, где касательная параллельна прямой
, в точке, где касательная параллельна прямой  . Сделать чертёж.
. Сделать чертёж.
Задание №5. Провести полное исследование функции и построить её график:
 .
.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а)  , б)
, б)  , в)
, в)  .
.
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б)  .
.
Задание №8. Найти несобственный интеграл  .
.
Задание №9. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

 .
.
Демонстрационный вариант для контрольной работы №2
Задание №1. Исследовать функцию на непрерывность. Найти точки разрыва и определить их тип. Сделать чертёж.


Задание №2. Найти производные функций:
 а)
а)  , б)
, б)  , в)
, в) 
Задание №3. Вычислить предел  с помощью правила Лопиталя.
с помощью правила Лопиталя.
Задание №4. Провести полное исследование функции  и построить её график.
и построить её график.
Задание №5. Пользуясь понятием дифференциала, найти приближённое значение  .
.
Задание №6. Найти неопределённые интегралы. Правильность полученных результатов проверить дифференцированием.
 а)
а)  , б)
, б)  , в)
, в) 
Задание №7. Найти определённые интегралы:
 а)
а)  , б)
, б)  .
.
Задание №8. Вычислить площадь плоской фигуры, ограниченной заданными линиями. Сделать чертёж.

 .
.
Задание №9. Найти несобственный интеграл 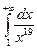 .
.
Решение демонстрационного варианта контрольной работы №2
Задача №1
Так как данная функция определена на всей числовой оси, то «подозрительными на разрыв» являются те точки, в которых изменяется аналитическое выражение функции. Т.е. точки х = -1 и х = 0. Вычислим односторонние пределы в этих точках.
Для точки х = -1 имеем
 ;
;
 .
.
Односторонние пределы функции в точке х = -1 существуют, но не равны между собой. Следовательно, эта точка является точкой разрыва первого рода.
Для точки х=0 получаем
 .
.
Односторонние пределы функции при  равны между собой и равны значению функции в точке х=0:
равны между собой и равны значению функции в точке х=0:  . Следовательно, исследуемая точка является точкой непрерывности.
. Следовательно, исследуемая точка является точкой непрерывности.
Построим график данной функции:
 |
Ответ: функция непрерывна на промежутке  и на промежутке
и на промежутке  ; точка х= -1 является точкой разрыва первого рода.
; точка х= -1 является точкой разрыва первого рода.
Задача №2
а) 

б)

в) 

Ответ: а)  , б)
, б) 
 , в)
, в) 
 .
.
Задача №3
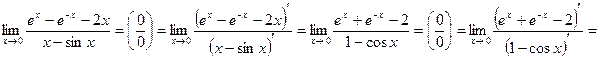

Правило Лопиталя было применено 3 раза.
Ответ: 2.
Задача №4
Исследовать и построить график функции 
Решение.
1. Область определения функции D(у)=  .
.
2. Находим точки пересечения графика функции с осями координат: если х=0, то у=0; если у=0, то х=0. Таким образом, график проходит через начало координат
3. Функция не является периодической, так как не существует такого положительного числа Т, что у(х+Т)=у(х).
4. Функция является нечётной, т.к.
1) область определения симметрична относительно начала координат, 2) у(-х)=  -у(х).
-у(х).
5. Определим асимптоты графика:
Точки х=  и х= -
и х= -  являются точками разрыва функции. Так как
являются точками разрыва функции. Так как  и
и  , то прямая х=
, то прямая х=  служит вертикальной асимптотой графика функции. Аналогично найдём односторонние пределы в точке х= -
служит вертикальной асимптотой графика функции. Аналогично найдём односторонние пределы в точке х= -  :
:
 и
и  , следовательно, прямая х= -
, следовательно, прямая х= -  также является вертикальной асимптотой графика функции.
также является вертикальной асимптотой графика функции.
б) горизонтальные асимптоты.
Для нахождения горизонтальной асимптоты вычислим предел функции на бесконечности:
 , итак, прямая у=0 – горизонтальная асимптота.
, итак, прямая у=0 – горизонтальная асимптота.
в) Наклонные асимптоты:
у=кх+b – уравнение наклонной асимптоты


наклонной асимптоты нет (она совпадает с горизонтальной у=0).
6. Исследуем функцию на монотонность и экстремум:
 ;
;
Найдём критические точки из условий  или
или  не существует:
не существует:
равенство 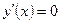 не выполняется ни при каких х;
не выполняется ни при каких х;
 не существует при х=
не существует при х=  и х= -
и х= -  .
.
Итак, критические точки: х=  и х= -
и х= -  .
.
Составим таблицу
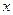 |  | 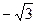 | 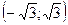 |  |  |
 | + | Не существует | + | Не существует | + |
    | Не существует | Не существует | |||
 | возрастает | возрастает | возрастает |
7. Исследуем функцию на выпуклость и вогнутость, найдём точки перегиба:

 .
.
Определим критические точки для второй производной:
 , т.е.
, т.е.  , откуда
, откуда  ;
;
 не существует при
не существует при  .
.
Составим таблицу:
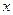 |  | 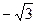 |  |  | 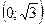 |  |  |
 | + | Не существует | _ |  | + | Не существует | _ |
 |  | Не существует |  | Не существует | |||
 | вогнутая | выпуклая | Точка перегиба | вогнутая | выпуклая |
8. Найдём значения функции в некоторых точках:  ,
,  ,
,  ,
,  .
.
9. Построим график функции
 |
Задача №5
Примем  ;
;  .
.
Тогда для вычисления воспользуемся формулой  . Найдём производную
. Найдём производную  .
.
 ,
,  . Перейдём к радианному измерению угла:
. Перейдём к радианному измерению угла:  , где
, где  - градусное измерение, тогда
- градусное измерение, тогда
 ;
;
 ;
;
 ;
;  ;
;


Ответ: 
 .
.
Задание №6
а) 
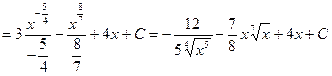 .
.
б) I способ: подведение под знак дифференциала

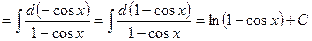 .
.
II способ: метод подстановки
 =
= 
Проверим результат дифференцированием: 
 . Получили подынтегральную функцию, что и требовалось доказать (ч.т.д.).
. Получили подынтегральную функцию, что и требовалось доказать (ч.т.д.).
в)  =
=  для вычисления интеграла
для вычисления интеграла  воспользуемся методом интегрирования по частям
воспользуемся методом интегрирования по частям 

Проверим результат дифференцированием: 
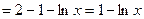 . Получили подынтегральную функцию, ч.т.д.
. Получили подынтегральную функцию, ч.т.д.
Ответ: а) 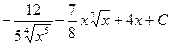 , б)
, б) 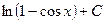 , в)
, в)  .
.
Задание №7
а) 
Решение.

 .
.
б) 
Решение.

 .
.
Ответ: а) 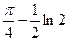 , б)
, б)  .
.
Задание №8

Сделаем чертёж фигуры:
 |

Ответ:  ; см. рис..
; см. рис..
Задание №9
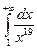
Решение. По определению несобственного интеграла находим:
 .
.
Ответ:  .
.
 2015-10-22
2015-10-22 1047
1047






