Из курса геометрии известно, что в прямоугольной декартовой системе координат уравнение прямой с угловым коэффициентом 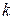 , проходящем через точку
, проходящем через точку 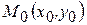 имеет вид:
имеет вид:
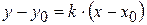 . (1)
. (1)
Поэтому, подставив в уравнение (1) 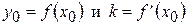 , получим уравнение касательной к кривой
, получим уравнение касательной к кривой 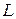 в точке
в точке 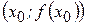 :
:
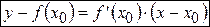 . (2)
. (2)
Как известно, условием перпендикулярности прямых, задаваемых уравнениями с угловыми коэффициентами 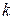 и
и 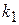 , является условие
, является условие 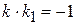 . Следовательно, уравнение нормали к кривой
. Следовательно, уравнение нормали к кривой 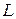 в точке
в точке 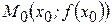 имеет вид:
имеет вид:
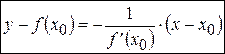 . (3)
. (3)
Замечание: Уравнение (3) задает нормаль к графику 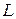 функции
функции 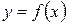 в точке
в точке 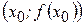 , если существует отличная от нуля производная
, если существует отличная от нуля производная 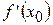 .
.
Если 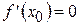 , то касательная к кривой
, то касательная к кривой 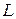 в такой точке будет параллельна оси
в такой точке будет параллельна оси 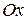 , а ее уравнение будет иметь вид:
, а ее уравнение будет иметь вид: 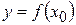 . Из определения же нормали следует, что нормаль к кривой
. Из определения же нормали следует, что нормаль к кривой 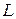 в такой точке будет перпендикулярна оси
в такой точке будет перпендикулярна оси 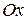 , а ее уравнение имеет вид
, а ее уравнение имеет вид 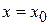 .
.
Если же 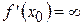 , то касательная к кривой
, то касательная к кривой 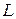 в такой точке параллельна оси
в такой точке параллельна оси 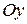 и ее уравнение имеет вид
и ее уравнение имеет вид 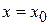 , а нормаль параллельна оси
, а нормаль параллельна оси 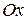 и ее уравнение имеет вид
и ее уравнение имеет вид 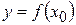
Примеры: Найти уравнения касательной и нормали к кривым:
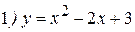 в точке с абсциссой
в точке с абсциссой 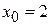
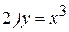 в точке с абсциссой
в точке с абсциссой 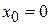
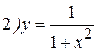 в точке с абсциссой
в точке с абсциссой 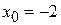
Решение:
1) Найдем значение функции 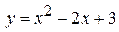 в точке с
в точке с 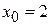 :
: 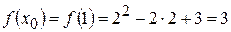 .
.
Далее найдем производную этой функции: 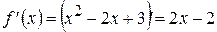 . Теперь найдем
. Теперь найдем 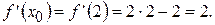
Составим уравнение касательной, для этого подставим найденные значения 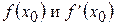 в уравнение (2):
в уравнение (2):
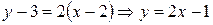 – уравнение касательной
– уравнение касательной
Составим уравнение нормали, для этого подставим найденные значения 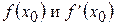 в уравнение (3):
в уравнение (3):
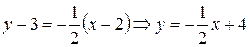 – уравнение нормали.
– уравнение нормали.
2) Найдем значение функции 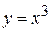 в точке с абсциссой
в точке с абсциссой 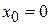 :
:
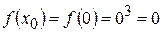 .
.
Найдем значение производной 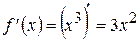 в точке
в точке 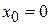 :
:
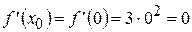 .
.
Так как 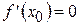 , то по замечанию уравнение касательной примет вид
, то по замечанию уравнение касательной примет вид 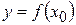 , то есть
, то есть 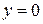 , а уравнение нормали
, а уравнение нормали 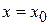 , то есть
, то есть 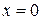 .
.
3) Найдем значение функции 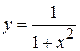 в точке с абсциссой
в точке с абсциссой 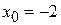
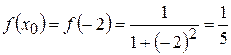 .
.
Теперь найдем значение производной:
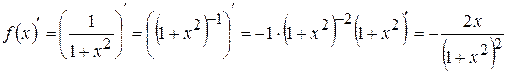 ,
,
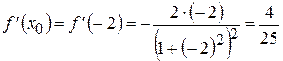 .
.
Подставив найденные значения 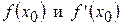 в уравнение (2) получим уравнение касательной:
в уравнение (2) получим уравнение касательной:
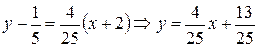 – уравнение касательной.
– уравнение касательной.
Подставив найденное значение в уравнение (3) получим уравнение нормали:
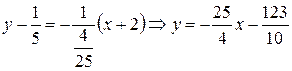 – уравнение нормали.
– уравнение нормали.
Упражнения:
1) В какой точке касательная к кривой 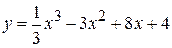 параллельна прямой
параллельна прямой 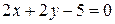 .
.
2) В какой точке касательная к кривой 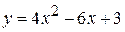 перпендикулярна прямой
перпендикулярна прямой 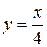 .
.
3) Кривая задана уравнением 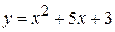 . Определить углы наклона касательных к положительному направлению оси
. Определить углы наклона касательных к положительному направлению оси 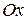 , проведенных к кривой в точках с абсциссами
, проведенных к кривой в точках с абсциссами 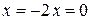 .
.
4) Найти угловой коэффициент касательной, проведенной к кривой 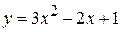 в точке
в точке 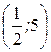 .
.
5) Составить уравнение касательной и нормали к кривым в данных точках с абсциссами:
а) 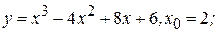
б) 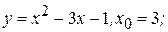
в) 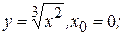
г) 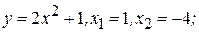
д) 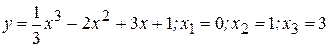 .
.
6) Найти координаты точки, в которой касательная к параболе 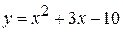 образует угол в 135о с осью
образует угол в 135о с осью 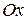 .
.
7) Найти скорость тела, движущегося по закону 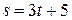 .
.
8) Тело движется прямолинейно по закону 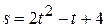 . Найти скорость тела в моменты
. Найти скорость тела в моменты 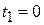 ,
, 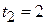 и
и 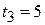 .
.
9) Найти скорость движения тела в момент времени 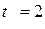 , если закон движения задан формулой:
, если закон движения задан формулой: 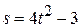 .
.
10) Когда скорость точки, движущейся прямолинейно по закону 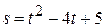 , равна нулю?
, равна нулю?
11) Какой угол образует с осью абсцисс касательная к параболе 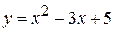 , проведенная в точке
, проведенная в точке 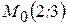 ? Составить уравнение этой касательной.
? Составить уравнение этой касательной.
12) Найти угол наклона касательной к кубической параболе 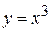 в точках с абсциссами
в точках с абсциссами 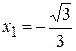 ,
, 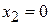 и
и 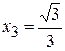 .
.
13) Какой угол образует с осью абсцисс касательная к кривой 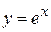 в точке
в точке 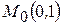 ?
?
 2015-05-30
2015-05-30 39802
39802
