«Кратные интегралы»
В состав расчетно-графической работы входят пять заданий по темам, изучаемым в третьем семестре второго курса: вычисление, геометрические и механические приложения двойных и тройных интегралов, вычисление криволинейных интегралов, поверхностных интегралов, определение характеристик (поток, дивергенция, циркуляция, вихрь) векторного поля.
Вариант 1
1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г
Z = x2 + y2 – 12x + 16y
Г: x= 0, y = 0, x + y = 1
2. Изменить порядок интегрирования в двойном интеграле.
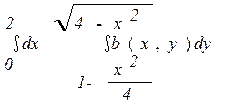
Сделать чертеж области интегрирования.
3. Найти координаты центра тяжести однородного тела, ограниченного поверхностями

2 – z = x2 + y2, z = 0
4. Вычислить криволинейный интеграл 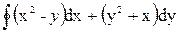 по замкнутому контуру С = ОАВО, где О – начало координат; ОА – отрезок оси ОХ; ВО – отрезок оси ОУ; линия АВ дана уравнением x + y-1 = 0.
по замкнутому контуру С = ОАВО, где О – начало координат; ОА – отрезок оси ОХ; ВО – отрезок оси ОУ; линия АВ дана уравнением x + y-1 = 0.
Вычисление провести двумя способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 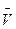 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OX. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OX. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру; б) по теореме Стокса.
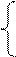
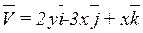 Г:
Г: 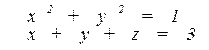
Вариант 2
1. Найти наибольшее и наименьшее значение функции
Z= x2+4xy-y2-6x-2y
в замкнутом треугольнике, ограниченном осями координат и прямой 2x + 3y – 6 = 0
2. Изменить порядок интегрирования в двойном интеграле
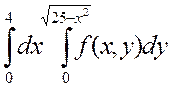
Сделать чертеж области интегрирования.
3. Найти массу тела, ограниченного плоскостью z = 0, цилиндром x2+y2=R2 и конусом z= 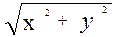 , если плотность в каждой его точке численно равна расстоянию от этой точки до оси oz.
, если плотность в каждой его точке численно равна расстоянию от этой точки до оси oz.
4. Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U с помощью криволинейного интеграла
(sin2y-ysin2x) dx + (xsin2y+cos2x+1) dy
5. Найти циркуляцию векторного поля 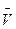 по контуру
по контуру 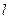 . Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя интеграл векторного поля по контуру £; б) по теореме Стокса
. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя интеграл векторного поля по контуру £; б) по теореме Стокса

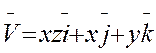
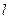 :
: 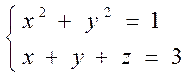
Вариант 3
1. Найти наибольшее и наименьшее значения функции
Z=x2+2xy-y2-4x в треугольниками со сторонами y=x+1, y=0,x=3
2. Изменить порядок интегрирования в двойном интеграле
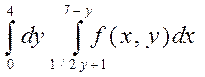
Сделать чертеж области интегрировании
3. Найти координаты центра тяжести однородного тела, ограниченного параболоидом x2 + 4z2 = 4y и плоскостью y = 2
4. Вычислить криволинейный интеграл 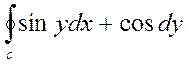 по замкнутому контуру С = ОАВО; где О-начало координат;ОА-отрезок оси ОХ; ВО- отрезок оси ОУ; линия АВ дана уравнением
по замкнутому контуру С = ОАВО; где О-начало координат;ОА-отрезок оси ОХ; ВО- отрезок оси ОУ; линия АВ дана уравнением 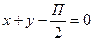
Вычисление провести двумя способами: непосредственно и по формуле Грина
5. Вычислить поток поля вектора 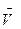 через треугольник, вырезанный из плоскости x+y+2z-2=0 координатными плоскостями, в том направлении к плоскости, которое образует с осью ОУ острый угол
через треугольник, вырезанный из плоскости x+y+2z-2=0 координатными плоскостями, в том направлении к плоскости, которое образует с осью ОУ острый угол
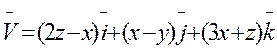
Вариант 4
1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г
Z=x2-2xy-y2-4x; T: y=x+1, y=0, x=3
2. Изменить порядок интегрирования в двойном интеграле
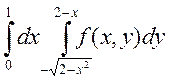
Сделать чертеж области интегрирования.
3. Найти центр тяжести однородного тела, ограниченного поверхностями: x =0, y=0, z=0, x+y+z=8
4. Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.
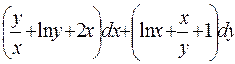
5. Найти циркуляцию векторного поля 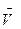 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса
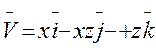 F:
F: 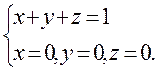
Вариант 5
1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г
Z=x2-2xy-2y2-4x+6y+3 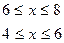
2. Изменить порядок интегрирования в двойном интеграле
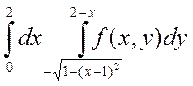
Сделать чертеж области интегрирования
3. Найти центр тяжести однородного тела, ограниченного плоскостями x = 0, y = 0, z = 0, 6x+3y+2z-6=0
4. Поверить, является ли заданное выражение дифференциалом некоторой функции (x,y) и в случае положительного ответа найти И(x,y) с помощью криволинейного интеграла.
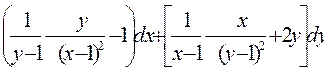
5. Найти циркуляцию векторного поля 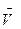 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисление провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисление провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса
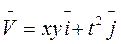 Г:
Г: 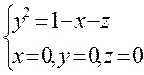 (1-ый октант)
(1-ый октант)
Вариант 6
1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г.
Z=2xy – 3x2 – 3y2+4x+4y+4
Г: 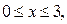
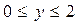
2. Изменить порядок интегрирования в двойном интеграле
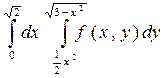
Сделать чертеж области интегрирования
3. Найти момент инерции относительно оси ОУ материальной пластинки, ограниченной линиями y=x, y=2x, xy=1, если поверхностная плоскость δ(x,y) =y2
4. Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.
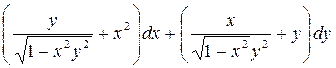
5. Найти циркуляцию векторного поля 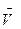 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
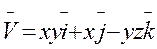 Г:
Г: 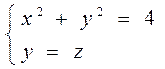
Вариант 7
1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г.
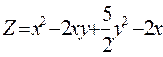 Г:
Г: 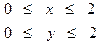
2. Изменить порядок интегрирования в двойном интеграле
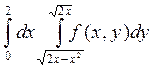
Сделать чертеж области интегрирования
3. Найти координаты центра тяжести однородной пластинки, ограниченной линиями: y = x, y =2x, xy = 1, x>0, y>0
4. Проверить, является ли заданное выражение дифференциалом некоторой функции U(x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.
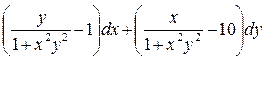
5. Найти циркуляцию векторного поля 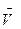 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б)по формуле Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б)по формуле Стокса.
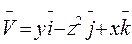 Г:
Г: 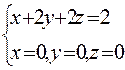
Вариант 8
1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г
Z=4x2 + 9y2-4x+6y+3
Г: x = 0,y = 0,x+y =1
2. Изменить порядок интегрирования в двойном интеграле
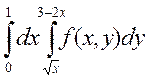
 Сделать чертеж области интегрирования.
Сделать чертеж области интегрирования.
3. Вычислить момент инерции относительно оси ОУ материальной пластинки, ограниченной линиями x-y = 2,y=x, если поверхностная область δ (x,y)=y.
4. Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла
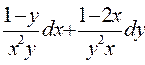
5. Найти циркуляцию векторного поля 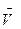 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ.Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по формуле Стокса
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ.Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по формуле Стокса
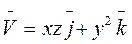 Г:
Г: 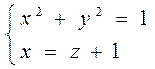
Вариант 9
1. Найти наименьшее и наибольшее значения функции двух переменных в замкнутой области D с заданными границами Г.
Z=x2 + 2xy-10
Г: y = x2-4,y = 0
2. Изменить порядок интегрирования в двойном интеграле
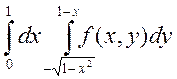
Сделать чертеж области интегрирования.
3. Найти координаты центра тяжести однородного тела, ограниченного поверхностями Z=y2 + x2, z = 4
4. Проверить, является ли заданное выражение дифференциалом некоторой функции U (x,y) и в случае положительного ответа найти U (x,y) с помощью криволинейного интеграла.
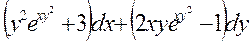
5. Найти циркуляцию векторного поля 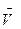 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
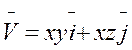 Г:
Г: 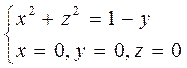
Вариант 10
1. Найти уравнение касательной плоскости и уравнение нормали
к поверхности x3y2 – xyz = 4; в точке А (2,1,2)
2. Изменить порядок интегрирования в интеграле

Область интегрирования изобразить на чертеже.
3. Определить цент тяжести однородного полушара
x2 + y2 + z2 = a2, z>0
4. Поле образовано силой F{y;a }, определить работу при перемещении массы по контуру, образованному полуосями координат и первой четвертью эллипса x = a cost, y = bsint
5. Дан вектор 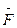 и плоскость Р. Плоскость [Р] вместе с координатными плоскостями образует поверхность некоторой пирамиды. Требуется:
и плоскость Р. Плоскость [Р] вместе с координатными плоскостями образует поверхность некоторой пирамиды. Требуется:
1. С помощью формулы Остроградского найти поток поля вектора через поверхность пирамиды в направлении внешней нормали.
2. Найти циркуляцию поля вектора 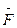 вдоль линии пересечения плоскости [Р] с координатными плоскостями непосредственно и по формуле Стокса, применяя в формуле Стокса за поверхность, по которой производится интегрирование, три грани пирамиды, лежащие в координатных плоскостях. При этом то направление обхода линии интегрирования следует считать положительным, при котором точка пробегает ее по ходу часовой стрелки, если смотреть от начала координат.
вдоль линии пересечения плоскости [Р] с координатными плоскостями непосредственно и по формуле Стокса, применяя в формуле Стокса за поверхность, по которой производится интегрирование, три грани пирамиды, лежащие в координатных плоскостях. При этом то направление обхода линии интегрирования следует считать положительным, при котором точка пробегает ее по ходу часовой стрелки, если смотреть от начала координат.
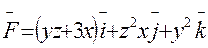

Вариант 11
1. Найти наименьшее и наибольшее значения функции двух переменных Z=5x2-3xy+y2+4
В замкнутой области D с заданными границами Г:
y=-1,x+y=1, x=-1
2. Изменить порядок интегрирования в двойном интеграле:
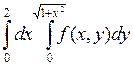
Сделать чертеж области интегрирования.
3. Найти момент инерции относительно своей оси однородного кругового цилиндра радиуса 2, высота 1.
4. Вычислить криволинейный интеграл 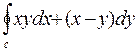 по замкнутому контуру С=ОАВО, где О-начало координат, ОА-отрезок оси ОХ, ВО-отрезок осиОУ, линия АВ дана своим уравнением x2 + y2-1 = 0
по замкнутому контуру С=ОАВО, где О-начало координат, ОА-отрезок оси ОХ, ВО-отрезок осиОУ, линия АВ дана своим уравнением x2 + y2-1 = 0
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 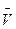 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
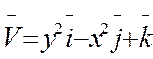 Г:
Г: 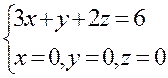
Вариант 12
1. Найти наименьшее и наибольшее значения функции двух переменных Z=x2+2xy-y2-2x+2y
В замкнутой области D с заданными границами Г:
y=x+2, y=0,x=2
2. Изменить порядок интегрирования в двойном интеграле:
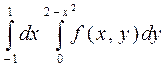
Сделать чертеж области интегрирования.
3. Найти центр тяжести однородного конического тела с радиусом основания 1 и высотой 2.
4. Вычислить криволинейный интеграл 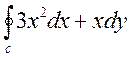 по замкнутому контуру С = ОАВО, где О - начало координат, ОА- отрезок оси ОХ, ВО-отрезок оси ОУ, линия АВ дана своим управлением x2+y2-4 = 0
по замкнутому контуру С = ОАВО, где О - начало координат, ОА- отрезок оси ОХ, ВО-отрезок оси ОУ, линия АВ дана своим управлением x2+y2-4 = 0
Вычисление провести 2 способами непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 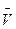 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г;
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г;
б) по теореме Стокса.
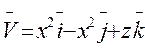 Г:
Г: 
Вариант 13
1. Найти наименьшее и наибольшее значения функции двух
переменных Z=10+2xy-x2
В замкнутой области D с заданными границами Г:
Y=4-x2, y=0
2. Изменить порядок интегрирования в двойном интеграле:
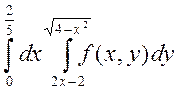
Сделать чертеж области интегрирования.
3. Найти момент инерции относительно оси вращения однородного параболического тела, ограниченного поверхностями
x2 + y2 =2-z, z=0, z=5
4. Вычислить криволинейный интеграл 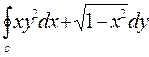 по замкнутому контуру С=ОАВО, где О –начало координат, ОА – отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением x2 + 4y2 – 1 = 0
по замкнутому контуру С=ОАВО, где О –начало координат, ОА – отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением x2 + 4y2 – 1 = 0
Вычисление провести двумя способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 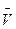 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисление провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисление провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
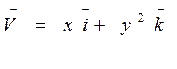 Г:
Г: 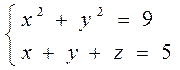
Вариант 14
1. Найти наименьшее и наибольшее значения функции дух переменных
Z=6xy-9x2-9y2+4x+4y
В замкнутой области D с заданными границами Г:
Г: 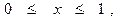
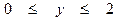
2. Изменить порядок интегрирования в двойном интеграле
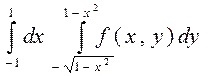
Сделать чертеж области интегрирования.
3. Найти центр тяжести однородного тела, ограниченного поверхностями x2+y2+z2=8; x2+y2-z2=0
4. Вычислить криволинейный интеграл 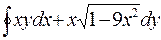 по замкнутому контуру С=ОАВО, где О-начало координат, ОА –отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением: 9x2 + y2 = 1
по замкнутому контуру С=ОАВО, где О-начало координат, ОА –отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением: 9x2 + y2 = 1
Вычисление провести двумя способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 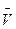 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.

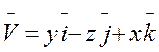 Г:
Г: 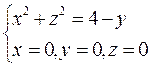 (1 октант)
(1 октант)
Вариант 15
1. Найти наименьшее и наибольшее значения двух переменных
Z=4x+2y+4x2+y2+6
В замкнутой области D с заданными границами Г: x=0,y=o.x+y+2=0
2. Изменить порядок интегрирования в двойном интеграле:
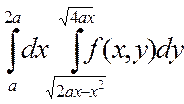
Сделать чертеж области интегрирования.
3. Вычислить момент инерции относительно вертикального диаметра однородной верхней половины шара радиуса 3.
4. Вычислить криволинейный интеграл 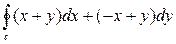 по замкнутому контуру С=ОАВО, где О –начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением x2 – 3x + 2 – y = 0
по замкнутому контуру С=ОАВО, где О –начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением x2 – 3x + 2 – y = 0
Вычисление провести 2 способами: а) непосредственно; б) по формуле Грина.
5. Найти циркуляцию векторного поля 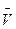 по контуру Г.Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г.Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
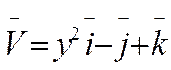 Г:
Г: 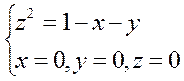
Вариант 16
1. Найти наименьшее и наибольшее значения функции двух переменных Z=x2-2xy-y2+4x+1
В замкнутой области D с заданными границами Г: x+y+1=0,y=0,x=-3
2. Изменить порядок интегрирования в двойном интеграле
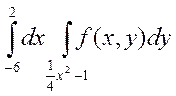
Сделать чертеж области интегрирования.
3. Найти центр тяжести однородной полукруглой пластинки радиуса 5.
4. Вычислить криволинейный интеграл 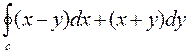 по замкнутому контуру С=ОАВО где, О –начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением
по замкнутому контуру С=ОАВО где, О –начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением 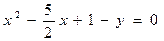
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 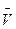 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
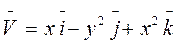 Г:
Г: 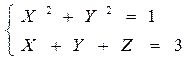
Вариант 17
1. Найти наименьшее и наибольшее значения функции двух переменных Z=2x2-4xy+5y2-8x+6
В замкнутой области D с заданными границами Г:
0 ≤ x ≤ 4, 0 ≤ y ≤ 4
2. Изменить порядок интегрирования в двойном интеграле
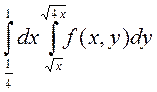
Сделать чертеж области интегрирования.
3. Найти центр тяжести однородной пластинки, ограниченной кардиоидой  ρ = 2(1+COSφ)
ρ = 2(1+COSφ)
4. Вычислить криволинейный интеграл 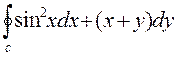 по замкнутому контуру С=ОАВО, где О –начало координат, ОА – отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением cosx – y = 0
по замкнутому контуру С=ОАВО, где О –начало координат, ОА – отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением cosx – y = 0
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 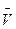 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
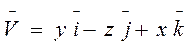 Г:
Г: 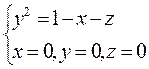 (1 октант)
(1 октант)
Вариант 18
1. Найти наименьшее и наибольшее значения функции двух переменных Z=x2+xy-2
В замкнутой области D с заданными границами Г: y=4x-4, y=0
2. Изменить порядок интегрирования в двойном интеграле
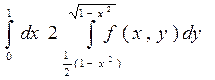
Сделать чертеж области интегрирования.
3. Найти момент инерции однородной четверти круга радиуса 5. Относительно оси ОХ.
4. Вычислить криволинейный интеграл 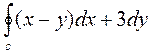 по замкнутому контуру С=ОАВО, где О- начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением: 2cosx – y = 0
по замкнутому контуру С=ОАВО, где О- начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением: 2cosx – y = 0
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 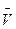 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
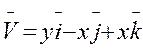 Г:
Г: 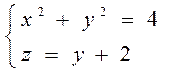
Вариант 19
1. Найти наименьшее и наибольшее значения функции
Z = 2x2 + 2xy - ½y2 - 4x
В замкнутой области D с заданными границами Г: y=2x,y=2,x=0
2. Изменить порядок интегрирования в двойном интеграле:
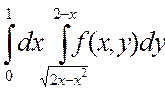
Сделать чертеж области интегрирования.
3. Найти центр тяжести однородной пластинки, ограниченной линиями y = x2, y = 1 – x2
4. Вычислить криволинейный интеграл 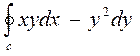 по замкнутому контуру С=ОАВО, где О- начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением: x + y – 2 = 0
по замкнутому контуру С=ОАВО, где О- начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением: x + y – 2 = 0
Вычисление провести 2 способами: непосредственно и по теореме Грина.
5. Найти циркуляцию векторного поля 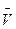 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами непосредственно: а) вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами непосредственно: а) вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
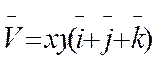 Г:
Г: 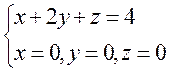
Вариант 20
1. Найти наименьшее и наибольшее значения функции двух переменных Z=5x2+8xy+5y2-18x-18y
В замкнутой области D с заданными границами Г:
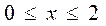
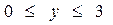
2. Изменить порядок интегрирования в двойном интеграле.
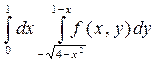
Сделать чертеж области интегрирования.
3. Найти момент инерции относительно диаметра однородного кольца с внутренним радиусом 1 и внешним радиусом 3.
4. Вычислить криволинейный интеграл 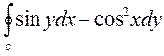 по замкнутому контуру С=ОАВО, где О- начало координат, ОА- отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением x + y – π
по замкнутому контуру С=ОАВО, где О- начало координат, ОА- отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением x + y – π  = 0
= 0
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 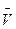 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести двумя способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
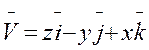 Г:
Г: 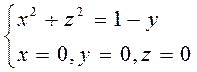
Вариант 21
1. Найти наименьшее и наибольшее значения функции двух переменных Z=5x2-3xy+y2+4
В замкнутой области D с заданными границами Г:
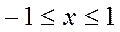

2. Изменить порядок интегрирования в двойном интеграле
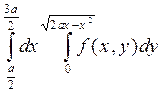
Сделать чертеж области интегрирования.
3. Вычислить массу пластинки, ограниченной линиями 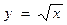 ,
, 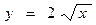 , x = 4, если ее плоскость
, x = 4, если ее плоскость  μ = x
μ = x
4. Вычислить криволинейный интеграл 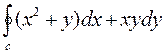 по замкнутому кругу С=ОАВО, где О – начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением y – x2 + 1 = 0
по замкнутому кругу С=ОАВО, где О – начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением y – x2 + 1 = 0
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 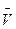 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
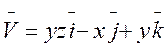 Г:
Г: 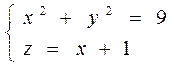
Вариант 22
1. Найти наименьшее и наибольшее значения функции двух переменных Z=x2+2xy+4x-y2
В замкнутой области D с заданными границами Г: x+y+2=0,x=0,y=0
2. Изменить порядок интегрирования в двойном интеграле:
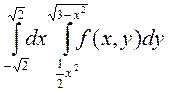
Сделать чертеж области интегрирования.
3. Найти центр тяжести однородного тела, ограниченного конусом
Z = 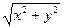 и плоскостью Z = 2
и плоскостью Z = 2
4. Вычислите криволинейный интеграл 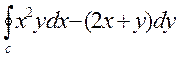 по замкнутому контуру С=ОАВО, где О – начало координат, ОА – отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением 2 – 3x2 – y = 0
по замкнутому контуру С=ОАВО, где О – начало координат, ОА – отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением 2 – 3x2 – y = 0
Вычисления провести 2 способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 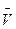 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
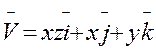 Г:
Г: 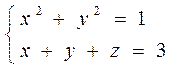
Вариант 23
1. На поверхности x2 + y2 + z2 – 6y + 4z = 12 найти точки, в которых касательная плоскость параллельна координатной плоскости 1/ХОУ, 2/ УОZ.
2. Изменить порядок интегрирования в интеграле
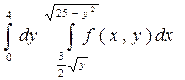
Область интегрирования изобразить на чертеже.
3. Определить массу тела, ограниченного поверхностями
2x + z = 2a, x + z = a, y2 = ax, y = 0 при y >0, если плотность в каждой его точке равна ординате у этой точки.
4. Написать и проверить формулу Грина для 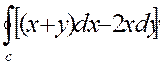 по контуру треугольника со сторонами x = 0,y = 0,x + y = a
по контуру треугольника со сторонами x = 0,y = 0,x + y = a
5. Дан вектор 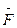 и плоскость Р. Плоскость Р вместе с координатными плоскостями образует поверхность некоторой пирамиды. Требуется:
и плоскость Р. Плоскость Р вместе с координатными плоскостями образует поверхность некоторой пирамиды. Требуется:
а) С помощью формулы Остроградского найти поток поля вектора 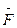 через поверхность пирамиды в направлении внешней нормали;
через поверхность пирамиды в направлении внешней нормали;
б) Найти циркуляцию поля вектора 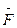 вдоль линии пересечения плоскости Р с координатными плоскостями непосредственно и по формуле Стокса, применяя в формуле Стокса за поверхность, по которой производится интегрирование, три грани пирамиды, лежащие в координатных плоскостях. При этом направление обхода линии интегрирования следует считать положительным, при которой точка пробегает по ее ходу часовой стрелки, если смотреть от начала координат.
вдоль линии пересечения плоскости Р с координатными плоскостями непосредственно и по формуле Стокса, применяя в формуле Стокса за поверхность, по которой производится интегрирование, три грани пирамиды, лежащие в координатных плоскостях. При этом направление обхода линии интегрирования следует считать положительным, при которой точка пробегает по ее ходу часовой стрелки, если смотреть от начала координат.
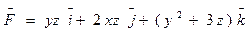 (Р) 2x + y + 3z = 6
(Р) 2x + y + 3z = 6
Вариант 24
1. Найти наибольшее и наименьшее значения функции
Z=x2+2xy-10 в замкнутой области, ограниченной параболой
Y = x2 – 4 и осью OX.
2. Найти порядок интегрирования в двойном интеграле:
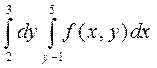
Сделать чертеж области интегрирования.
3. Найти центр тяжести однородного тела, ограниченной параболоидом y2 + z2 + = x и плоскостью x = 2
4. Вычислить криволинейный интеграл 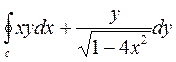 по замкнутому кругу С=АОВО, где О –начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением:
по замкнутому кругу С=АОВО, где О –начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением:
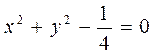
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5.Найти поток векторного поля 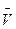 через замкнутую поверхность δ. Нормаль кδ выбирается внешняя. Вычисление провести 2 способами: непосредственно, найти сумму потоков через все части поверхности и по теореме Остроградского.
через замкнутую поверхность δ. Нормаль кδ выбирается внешняя. Вычисление провести 2 способами: непосредственно, найти сумму потоков через все части поверхности и по теореме Остроградского.
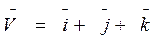
δ: z2 = x2 + y2, z≥0, z = 2
Вариант 25
1. Найти наименьшее и наибольшее значения функции
Z=x2+2xy-y2-2x+2y в треугольнике со сторонами y=x+2, y=0, x=2
2. Изменить порядок интегрирования в двойном интеграле:
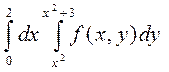
Сделать чертеж области интегрирования.
3. Найти массу тела, ограниченного плоскостью z=0, цилиндром x2+y2=R2 и конусом z = 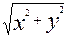 , если плотность в каждой ее точке численно равна расстоянию от точки до оси OZ.
, если плотность в каждой ее точке численно равна расстоянию от точки до оси OZ.
4. Вычислить криволинейный интеграл 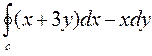 по замкнутому контуру С=ОАВО, где О-начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением
по замкнутому контуру С=ОАВО, где О-начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением 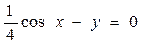
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти поток векторного поля 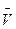 через замкнутую поверхность δ. Нормаль кδ выбирается внешняя. Вычисления провести 2 способами: непосредственно, найти сумму потоков через все части поверхности и по теореме Остроградского.
через замкнутую поверхность δ. Нормаль кδ выбирается внешняя. Вычисления провести 2 способами: непосредственно, найти сумму потоков через все части поверхности и по теореме Остроградского.
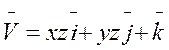
δ: x2+y2=1, z=2, x≥0, y≥0,z≥0
Вариант 26
1. Найти наибольшее и наименьшее значения функции
Z=6xy-9x2-9y2+4x+4y в прямоугольнике 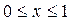 ,
, 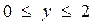
2. Изменить порядок интегрирования в двойном интеграле6
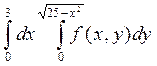
Сделать чертеж области интегрирования
3. Найти момент инерции пирамиды, ограниченной координатными плоскостями и плоскостью 2x + 3y + 3z = 6 относительно оси OZ, если в каждой ее точке плотность численно равна аппликате этой точки.
4. Вычислить криволинейный интеграл 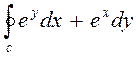 по замкнутому контуру С=ОАВО, где О – начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением: 2x + y – 4 = 0
по замкнутому контуру С=ОАВО, где О – начало координат, ОА- отрезок оси ОХ, ВО- отрезок оси ОУ, линия АВ дана своим уравнением: 2x + y – 4 = 0
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти поток векторного поля 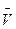 через замкнутую поверхность δ. Нормаль кδ выбирается внешняя. Вычисление провести 2 способами: а) непосредственно, найти сумму потоков через все части поверхности; б) по теореме Остроградского.
через замкнутую поверхность δ. Нормаль кδ выбирается внешняя. Вычисление провести 2 способами: а) непосредственно, найти сумму потоков через все части поверхности; б) по теореме Остроградского.
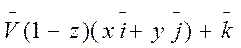
δ: (1-z)2=x2+y2 0≤z≤1, z=0
Вариант 27
1. Найти наименьшее и наибольшее значения функции двух переменных Z= x2-2xy-y2+4x+1
В замкнутой области D с заданными границами в треугольнике со сторонами x+y+1=0, y=0,x=-3
2. Вычислить площадь, ограниченную линиями y=sinx, y=cosx, x=0
3. Найти центр тяжести однородного тела параболоидом x2+4z2=4y и плоскостью y=2.
4. Вычислить криволинейный интеграл 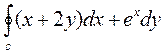 по замкнутому контуру С=ОАВО, где О –начало координат, ОА- отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением 3 – x2 – y = 0.
по замкнутому контуру С=ОАВО, где О –начало координат, ОА- отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением 3 – x2 – y = 0.
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти циркуляцию векторного поля 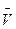 по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
по контуру Г. Направление на контуре выбрать против часовой стрелки, если смотреть с положительного направления оси OZ. Вычисления провести 2 способами: а) непосредственно, вычисляя линейный интеграл векторного поля по контуру Г; б) по теореме Стокса.
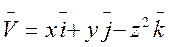
Г:  x2 + y2 + z2 = 1, x≥0, y≥0, z≥0
x2 + y2 + z2 = 1, x≥0, y≥0, z≥0
Вариант 28
1. Найти наибольшее и наименьшее значения функции в замкнутой области Z=2x2+2xy-½y2-4x в треугольнике со сторонами y=2x, y=2, x=0
2. Вычислить площадь, ограниченную линиями: y2=a2-ax, y=a+x
3. Найти массу тела, ограниченного координатными плоскостями и плоскостью x + y + z = 1, если плотность в каждой его точке численно равна произведению координат этой точки.
4. Вычислить криволинейный интеграл 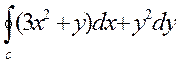 по замкнутому контуру С=ОАВО, где О- начало координат, ОА- отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением x+3y-6=0
по замкнутому контуру С=ОАВО, где О- начало координат, ОА- отрезок оси ОХ, ВО – отрезок оси ОУ, линия АВ дана своим уравнением x+3y-6=0
Вычисление провести 2 способами: непосредственно и по формуле Грина.
5. Найти поток векторного поля 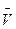 через замкнутую поверхность δ нормаль кδ выбирается внешняя, найдя сумму потоков через все части поверхности и по теореме Остроградского.
через замкнутую поверхность δ нормаль кδ выбирается внешняя, найдя сумму потоков через все части поверхности и по теореме Остроградского.
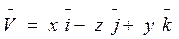
δ: x2+y2+z2=4, x≥0, y≥0,z≥0
Вариант 29
1. Найти наибольшее и наименьшее значения функции в замкнутой области Z=5x2-3xy+y2+4 в квадрате -1≤x≤1, -1≤y≤1
2. Вычислить площадь, ограниченную линиями:
r=4(1+cosφ) rcosφ=3 (справа от прямой)
3. Найти центр тяжести однородного тела, ограниченного поверхностями x2 + y2 = 4 – z, z = 0
4. Доказать, что заданное выражение является полным дифференциалом некоторой функции И(x,y) и найти И(x,y)
2(2x3-3xy2+y2)dx+2y(2x-3x2-2y2)dy
5. Найти поток векторного поля 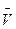 через замкнутую поверхность S нормаль к S выбирается внешняя. Вычисления провести 2 способами: непосредственно, найдя сумму потоков через все части поверхности и по теореме Остроградского.
через замкнутую поверхность S нормаль к S выбирается внешняя. Вычисления провести 2 способами: непосредственно, найдя сумму потоков через все части поверхности и по теореме Остроградского.
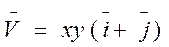
S: z = 4-x2-y2, z = 0
Вариант 30
1. Найти наименьшее и наибольшее значения функции в замкнутой области Z=x2+2xy+4x-y2 в треугольнике со сторонами x+y+2=0,x=0,y=0
2. Вычислить площадь, ограниченную линиями: r = a(1-cosφ), r = a
и расположенную вне кардиоиды.
3. Найти центр тяжести однородного тела ограниченного поверхностями x2+y2=4, y+z=2, z=0
4. Доказать, что заданное выражение является полным дифференциалом некоторой функции U(x,y) и найти U
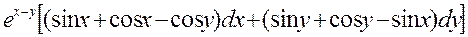
5. Найти поток векторного поля V через замкнутую поверхность S нормаль к поверхности S выбирается внешняя. Вычисления провести: a) непосредственно, найдя сумму потоков через все части поверхности; б) по теореме Остроградского.
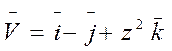 , S: 2z = x2 + y2, z = 2
, S: 2z = x2 + y2, z = 2
в
Надежда Николаевна Адамушко
Материалы расчетно-графической работы по математике
Кратные интегралы
учебно-методическое пособие
издание первое
Научный редактор: Балабан Е.И.
Технический редактор: Брыль С.В.
Подписано в печать 9.11.11
Печать лазерная. Усл.печ.лист.1
Заказ №008. Тираж 100 экз.
Отпечатано в МАМИ Коломна
 2015-10-22
2015-10-22 3240
3240








