Лабораторная работа № 3

Векторное произведение двух векторов.
Смешанное произведение трех векторов

1. Цель работы

Приобретение умений вычислять векторное и смешанное произведения векторов, решать задачи на геометрический и физический смысл.

2. Содержание работы

1) Вычислите векторное произведение векторов и (табл. 1). Решение оформите в тетради.

2) Вершины пирамиды находятся в точках A, B, C и D. Вычислите площадь указанной грани (табл. 2). Решение оформите в тетради.

3) Сила приложена к точке B. Найдите модуль момента силы относительно точки А (табл. 3). Решение оформите в тетради.

4) Вычислите смешанное произведение векторов , и (табл. 1). Являются ли они компланарными? Решение оформите в тетради.

5) Найдите объем пирамиды ABCD (табл. 2). Решение оформите в тетради и сдайте на проверку.

3. Общие сведения и примеры выполнения заданий

Векторным произведением вектора на вектор называется вектор , удовлетворяющий трем условиям:

1)

2) вектор одновременно ортогонален вектору и

3) направление вектора таково, что если смотреть с его конца, то поворот от к на угол j совершается против часовой стрелки (рис. 1).

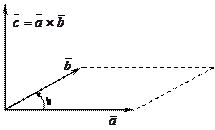Рис. 1

Свойства векторного произведения:

1) ,

2) т.т.т. – условие коллинеарности в векторной форме,

3) ,

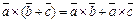4) .

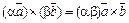Пусть векторы и , тогда координаты вектора вычисляются по формуле:

. (1)

Пример 1. Найдите координаты вектора , если , .

Решение. По формуле (1) получим:

.

Ответ: .

Геометрический смысл векторного произведения состоит в том, что его длина численно равна площади параллелограмма, построенного на векторах и как на сторонах, т.е.

. (2)

Отсюда следует, что площадь треугольника, двумя сторонами которого служат векторы и равна

. (3)

Пример 2. Найдите площадь треугольника с вершинами А (1; 2; 0), В (3; 2; 1), С (–2; 1; 2).

Решение. Найдем координаты любых двух векторов, имеющих общее начало. Например, и .

Теперь вычислим векторное произведение векторов и по формуле (1):

.

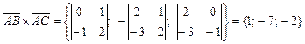Длина вектора 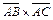равна:

.

Т.о. площадь D АВС по формуле (3) будет равна:

(кв. ед.).

Ответ: кв. ед.

Физический смысл векторного произведения состоит в том, что вращающий момент (ед. изм.: Ньютон×метр) относительно точки A силы , приложенной к точке B, представляет собой векторное произведение вектора на вектор (рис. 2), т.е.

(4)

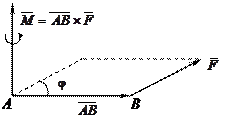Рис. 2

Пример 3. Сила приложена к точке B (0; 2; 1). Определите момент этой силы относительно точки A (–1; 2; 3).

Решение. Найдем координаты вектора : . Вычислим векторное произведение векторов и по формуле (1):

.

Согласно формуле (4) момент .

Ответ: .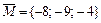

Смешанным произведением трех векторов , и называется число, обозначаемое и равное скалярному произведению вектора на вектор , т.е. .

Пусть векторы , и , тогда смешанное произведение вычисляется по формуле:

. (5)

Пример 4. Найдите смешанное произведение векторов , , .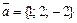

Решение. Согласно формуле (5) получим:

.

Ответ: .

Геометрический смысл смешанного произведения трех векторов состоит в том, что его модуль численно равен объему параллелепипеда, построенного на этих векторах как на ребрах (рис. 3):

. (6)

Если на трех векторах строить треугольную пирамиду, то:

. (7)

Рис. 3

Пример 5. Вычислите объем пирамиды с вершинами в точках A ₁(5; 1; –4), A ₂(1; 2; –1), A ₃(3; 3; –4), A ₄(2; 2; 2).

Решение. Найдем координаты трех векторов, имеющих общее начало. Например, , , .

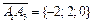По формуле (5) вычислим смешанное произведение этих векторов:

.

Тогда по формуле (7) объем пирамиды равен:

(куб. ед.).

Ответ: куб. ед.

Условием компланарности трех векторов является равенство:

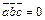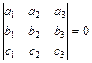или . (8)

Пример 6. Докажите, что три вектора , , 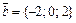компланарны.

Решение. Проверим выполнимость равенства (8):

. Что и требовалось доказать.

4. Индивидуальные задания

Таблица 1

№ вар.

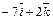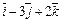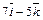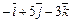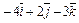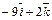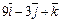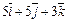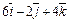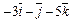Таблица 2

№ вар.	A	B	C	D	Грань
	(3; 4; 5)	(1; 2; 1)	(–2; –3; 6)	(3; –6; –3)	ACD
	(–7; –5; 6)	(–2; 5; –3)	(3; –2; 4)	(1; 2; 2)	BCD
	(1; 3; 1)	(–1; 4; 6)	(–2; –3; 4)	(3; 4; –4)	ACD
	(2; 4; 1)	(–3; –2; 4)	(3; 5; –2)	(4; 2; –3)	ABD
	(–5; –3; –4)	(1; 4; 6)	(3; 2; –2)	(8; –2; 4)	ACD
	(3; 4; 2)	(–2; 3; –5)	(4; –3; 6)	(6; –5; 3)	ABD
	(–4; 6; 3)	(3; –5; 1)	(2; 6;–4)	(2; 4; –5)	ACD
	(7; 5; 8)	(–4; –5; 3)	(2; –3; 5)	(5; 1; –4)	BCD
	(3; –2; 6)	(–6; –2; 3)	(1; 1; –4)	(4; 6; –7)	ABD
	(–5; –4; –3)	(7; 3; –1)	(6; –2; 0)	(3; 2; –7)	BCD
	(3; –5; –2)	(–4; 2; 3)	(1; 5; 7)	(–2; –4; 5)	ACD
	(7; 4; 9)	(1; –2; –3)	(–5; –3; 0)	(1; –3; 4)	ABD
	(–4; –7; –3)	(–4; –5; 7)	(2; –3; 3)	(3; 2; 1)	BCD
	(–4; –5; –3)	(3; 1; 2)	(5; 7; –6)	(6; –1; 5)	ACD
	(5; 2; 4)	(–3; 5; –7)	(1; –5; 8)	(9; –3; 5)	ABD
	(–6; 4; 5)	(5; –7; 3)	(4; 2; –8)	(2; 8; –3)	ACD
	(5; 3; 6)	(–3; –4; 4)	(5; –6; 8)	(4; 0; –3)	BCD
	(5; –4; 4)	(–4; –6; 5)	(3; 2; –7)	(6; 2; –9)	ABD
	(–7; –6; –5)	(5; 1; –3)	(8; –4; 0)	(3; 4; –7)	BCD
	(7; –1; –2)	(1; 7; 8)	(3; 7; 9)	(–3; –5; 2)	ACD
	(5; 2; 7)	(7; –6; –9)	(–7; –6; 3)	(1; –5; 2)	ABD
	(–2; –5; –1)	(–6; –7; 9)	(4; –5; 1)	(2; 1; 4)	BCD
	(–6; –3; –5)	(5; 1; 7)	(3; 5; –1)	(4; –2; 9)	ACD
	(7; 4; 2)	(–5; 3; –9)	(1; –5; 3)	(7; –9; 1)	ABD
	(–8; 2; 7)	(3; –5; 9)	(2; 4; –6)	(4; 6; –5)	ACD
	(4; 3; 1)	(2; 7; 5)	(–4; –2; 4)	(2; –3; –5)	ACD

Таблица 3

№ вар.		А	В
	{5; –3; 9}	(2; 6; 5)	(3; 4; –6)
	{–3; 1; –9}	(9; 5; –7)	(6; –3; 5)
	{2; 19; –4}	(6; –4; –1)	(5; 3; 4)
	{–4; 5; –7}	(7; 0; –3)	(4; –2; 3)
	{4; 11; –6}	(4; –2; –3)	(3; 5; 1)
	{3; –5; 7}	(0; 4; 3)	(2; 3; –5)
	{5; 4; 11}	(4; 2; –6)	(6; 1; –5)
	{–9; 5; 7}	(4; –3; 5)	(1; 6; –3)
	{6; 5; –7}	(4; 9; –6)	(7; –6; 4)

Продолжение табл. 3

№ вар.		А	В
	{–5; 4; 4}	(2; –4; 1)	(3; 7; –5)
	{4; 7; –3}	(8; 5; –4)	(5; –4; 2)
	{2; 2; 9}	(2; 4; 0)	(4; 2; –3)
	{9; –3; 4}	(4; 6; –5)	(–5; 4; –2)
	{5; –2; 3}	(2; –3; –6)	(7; 1; –5)
	{3; –5; 4}	(5; 6; –3)	(–3; 5; 9)
	{–10; 6; 5}	(4; 7; –5)	(4; –5; 9)
	{5; –3; 1}	(3; 8; –5)	(–5; 3; 7)
	{–5; 8; 4}	(0; 7; 4)	(2; –4; 7)
	{7; –5; 2}	(6; 4; –3)	(–3; 2; 0)
	{3; –4; 2}	(4; –1; –4)	(5; 3; –7)
	{4; –2; –5}	(4; 5; –3)	(–3; 2; –6)
	{7; 3; –4}	(4; –2; 11)	(–7; 2; 5)
	{9; –4; 4}	(4; –5; 9)	(5; –4; 3)
	{6; –4; 5}	(7; –3; 6)	(–5; –4; 2)
	{5; 5; –6}	(8; –1; 7)	(–9; 4; 7)
	{7; –6; 2}	(6; –2; 7)	(3; –6; 1)