а) невласні інтеграли з нескінченними границями
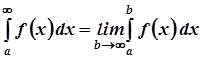 .
.
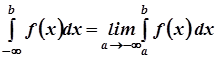 .
.
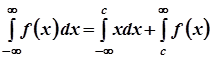 , де
, де 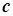 –довільне значення,
–довільне значення, 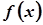 – всюди неперервна функція.
– всюди неперервна функція.
Якщо границя такого інтегралу є кінцевою, то такий інтеграл називається збіжним; у разі, коли інтеграл прямує до 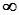 , його називають розбіжним.
, його називають розбіжним.
б) невласні інтеграли від розривних функцій
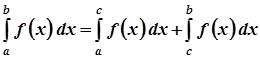 ,
,
де 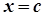 – точка розриву функції, де
– точка розриву функції, де
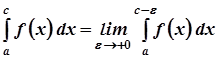 .
.
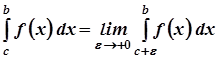 .
.
 2015-10-22
2015-10-22 229
229








