Ознаки збіжності додатних числових рядів

Необхідна умова збіжності

Якщо ряд збігається, то його загальний член 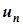прямує до нуля при 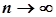, тобто .

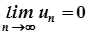Наслідок. Якщо 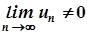, то ряд розбігається.

Ознака збіжності Даламбера

Якщ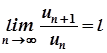о , то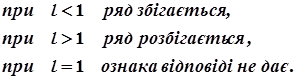

Гранична ознака порівняння

Нехай є два ряди , .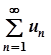

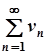Якщо 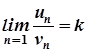, де 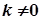, , 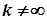то ці два ряди або одночасно збігаються, або одночасно розбігаються.

Такі ряди називають еквівалентними та позначають це так:

.

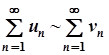Знакопочережні ряди

Числовий ряд називається знакопочережним, якщо його члени, що стоять поруч, мають різні знаки.

Такі ряди мають вигляд:

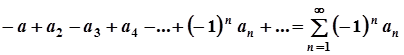, (1)

, (2)

де 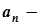абсолютна величина члена ряду.

Ознака Лейбніця

Якщо в знакопочережному ряді (2) члени такі, що

1)

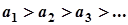
2) ,

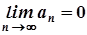то ряд збігається, а його сума за абсолютним значенням не перевершує перший член ряду.

Знакопочережний ряд називається умовно збіжним, якщо він збігається, а ряд, складений з абсолютних величин його членів, розбігається.

Знакопочережний ряд називається абсолютно збіжним, якщо збігається ряд з абсолютних величин його членів.