Диференціальним рівнянням (надалі, Д.Р.) називається рівняння, що містить похідні або диференціали невідомої функції. Найбільший порядок похідних називається порядком диференціального рівняння.
Д.Р. вигляду N1(y)M1(x)dx+M2(x)N2(y)dy=0 називаються Д.Р. з відокремленими змінними.
Д.Р. називається однорідним, якщо його можна подати у вигляді: 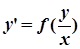 .
.
Воно за допомогою заміни змінної 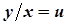 Þ
Þ 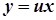 зводиться до Д.Р. з відокремлюваними змінними.
зводиться до Д.Р. з відокремлюваними змінними.
Д.Р. виду y’+P(x)y=Q(x) називається лінійним Д.Р. Його розв’язок розшукується у вигляді 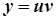 .
.
Приклад 1. Розв’язати задачу Коші (знайти загальний розв’язок диференційного рівняння і частинний розв’язок при заданих початкових умовах):

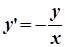 ,
, 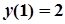 .
.
Розв’язання. Запишемо рівняння у диференціалах:
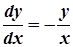 .
.
Дане рівняння є рівнянням першого порядку з відокремлюваними змінними (тобто може бути зведене до вигляду, коли з одного боку знака рівності присутня тільки залежна змінна y, а з іншого – тільки незалежна змінна x, таку рівність можна про інтегрувати і отримати загальний інтеграл рівняння).
Виконаємо відокремлення змінних, для чого домножимо рівняння на 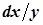 , в результаті отримаємо рівняння з відокремленими змінними
, в результаті отримаємо рівняння з відокремленими змінними
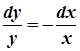 .
.
Проінтегруємо отримане рівняння:
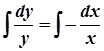 ,
,
і отримаємо
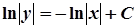 .
.
Це – загальний інтеграл рівняння у неявному вигляді. Звідси:
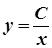 .
.
Частинний розв’язок знаходимо за допомогою початкової умови, підставляючи її о загального розв’язку:
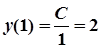 ; С= 2.
; С= 2.
Тоді частинним розв’язком диференційного рівняння є
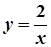 .
.
Приклад 2. Знайти частинний розв’язок диференційного рівняння при заданих початкових умовах

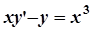 ,
, 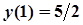 .
.
Розв’язання. Дане рівняння є лінійним диференційним рівнянням першого порядку.
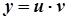 ;
; 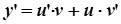 ;
;
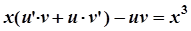 ,
,
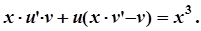
Накладемо на функцію v умову, щоб вираз у дужках дорівнював нулю, тобто
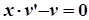 ,
,
і знайдемо функцію v з отриманого диференційного рівняння.
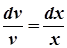
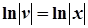 ,
, 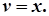
Тепер функцію u знаходимо з рівняння
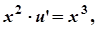
що утворюється в результаті підстановки v = x до початкового рівняння:
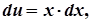
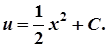
Оскільки y = uv, то загальним розв’язком рівняння є
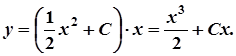
Константу інтегрування С знаходимо з початкової умови:
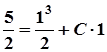 .
.
Отже, 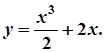
Приклад 3. Розв’яжіть задачу: знайти криву, яка проходить через точку М(0;1), якщо кутовий коефіцієнт дотичної в будь-якій точці кривої 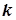 дорівнює
дорівнює 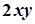 .
.
Розв’язання.
Як відомо, 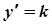 . Тому потрібно розв’язати задачу Коші:
. Тому потрібно розв’язати задачу Коші:
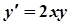 ,
, 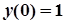 .
.
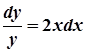 ,
, 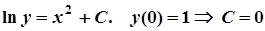 .
.
Отже, шукана крива 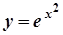 .
.
Рівняння вигляду 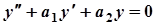 називаються лінійними однорідними Д.Р. Його загальний розв’язок має вигляд
називаються лінійними однорідними Д.Р. Його загальний розв’язок має вигляд 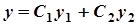 , де
, де 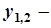 лінійно незалежні частинні розв’язки рівняння. Розшукуємо їх у вигляді
лінійно незалежні частинні розв’язки рівняння. Розшукуємо їх у вигляді 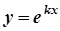 , де
, де 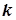 - корені характеристичного рівняння
- корені характеристичного рівняння 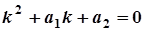 .
.
Розв’язок:
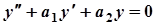
а) D>0 б) D=0, 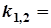 = –b/2
= –b/2
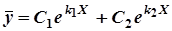 ;
; 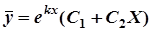 ;
;
в) D<0, 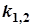 – комплексні числа.
– комплексні числа. 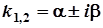
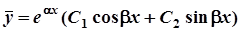 .
.
Рівняння вигляду 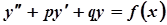 називається лінійним неоднорідним ДР 2-го порядку зі сталими коефіцієнтами.
називається лінійним неоднорідним ДР 2-го порядку зі сталими коефіцієнтами.
Для того, щоб знайти загальний розв’язок неоднорідного ДР, необхідно скористатися таким твердженням: загальний розв’язок такого ДР дорівнює сумі розв’язку відповідного однорідного ДР та якого-небудь частинного розв’язку неоднорідного ДР: 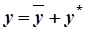 , де
, де 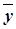 – загальний розв’язок відповідного однорідного ДР,
– загальний розв’язок відповідного однорідного ДР, 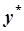 – частинний розв’язок неоднорідного ДР. Правила побудови
– частинний розв’язок неоднорідного ДР. Правила побудови 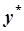 наведені у таблиці.
наведені у таблиці.
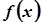 | 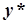 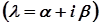 | |
| степенева частина відсутня | 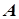 | 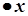 при при 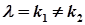 або або 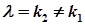 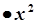 при при 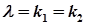 |
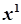 | 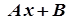 | |
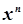 | 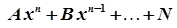 | |
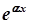 | 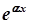 | |
показникова функція відсутня (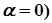 | показникова функція відсутня | |
лише 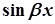 лише лише 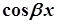 і і 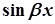 , і , і 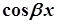 | і 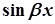 , і , і 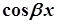 | |
тригонометричні функції відсутні (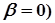 | тригонометричні функції відсутні |
Приклад 1. Розв’язати задачу Коші: 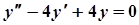 ,
, 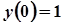 ,
, 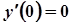 .
.
Розв’язання. Дане рівняння є лінійним однорідним ДР 2-го порядку зі сталими коефіцієнтами. Складемо характеристичне рівняння
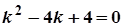 .
.
Дискримінант 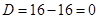 . Отже, рівняння має один дійсний корінь
. Отже, рівняння має один дійсний корінь 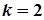 подвійної кратності. Тому загальний розв’язок ДР має вигляд
подвійної кратності. Тому загальний розв’язок ДР має вигляд
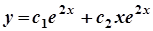 .
.
Для знаходження частинного розв’язку скористаємося початковими умовами. Для цього знайдемо 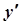 :
:
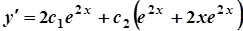 .
.
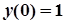
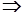
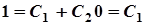 . Отже,
. Отже, 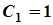 .
.
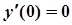
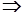
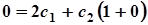 .
.
Отже, 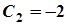 . Остаточно отримаємо
. Остаточно отримаємо 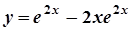 .
.
Приклад 2. Знайти загальний розв’язок лінійного неоднорідного диференціального рівняння зі сталими коефіцієнтами
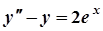 .
.
Розв'язання. 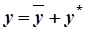 . Відповідне лінійне однорідне
. Відповідне лінійне однорідне 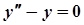 , характеристичне рівняння
, характеристичне рівняння 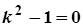 ,
, 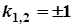 . Тоді загальний розв’язок лінійного однорідного ДР буде
. Тоді загальний розв’язок лінійного однорідного ДР буде 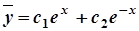 .
.
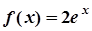 ,
, 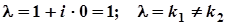 . Так як
. Так як 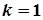 – корінь кратності
– корінь кратності 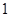 , то
, то 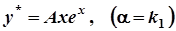 ,
,
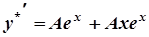 ,
, 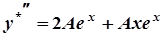 .
. 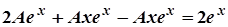 . Звідси
. Звідси 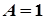 .
.
Тоді 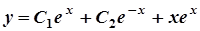 – загальний розв’язок шуканого рівняння.
– загальний розв’язок шуканого рівняння.
Приклад 3. Вказати вигляд (без обчислень коефіцієнтів)частинний розв’язок ЛНДР 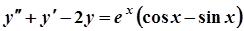 ..
..
Розв'язання. 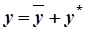 .
. 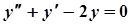 ,
, 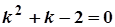 ,
, 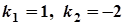 ,
, 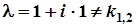
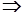
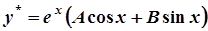 .
.
ЧИСЛОВІ РЯДИ
Нехай 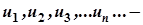 нескінченна послідовність чисел. Вираз
нескінченна послідовність чисел. Вираз 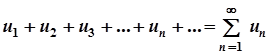 називається числовим рядом.
називається числовим рядом.
Ряд називається збіжним, якщо послідовність його часткових сум 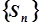 , де
, де 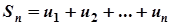 , має кінцеву границю, тобто
, має кінцеву границю, тобто 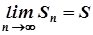 . Число
. Число 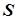 називається сумою ряду.
називається сумою ряду.
 2015-10-22
2015-10-22 1554
1554








