Первообразной функцией для функции f (x) называется такая функция F (x), производная которой равна данной функции, т.е. F' (x) = f (x).
Неопределенным интегралом от непрерывной функции f (x) или от дифференциального выражения f (x) dx называется совокупность первообразных функций f (x).
Обозначение:
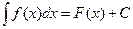 , где F' (x) = f (x). Функция f (x) называется подынтегральной функцией, а выражение f (x) dx – подынтегральным выражением.
, где F' (x) = f (x). Функция f (x) называется подынтегральной функцией, а выражение f (x) dx – подынтегральным выражением.
Свойства неопределенного интеграла:
Производная неопределенного интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.
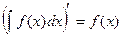 ; d
; d 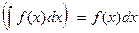 ;
;
Неопределенный интеграл от дифференциала функции f (x) равен функции f (x) с точностью до постоянного слагаемого
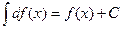 .
.
Постоянный множитель в подынтегральном выражении можно выносить за знак неопределенного интеграла
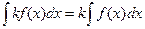 .
.
Неопределенный интеграл алгебраической суммы конечного числа функций равен алгебраической сумме неопределенных интегралов этих функций
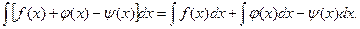
Таблица простейших неопределенных интегралов
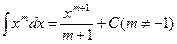 .
. 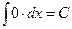 .
. 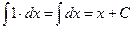 .
.
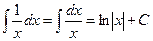 .
. 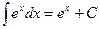 .
. 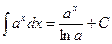 .
.
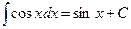 .
. 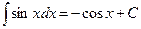 .
. 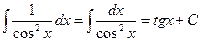 .
.
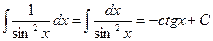 .
. 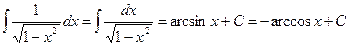 .
.
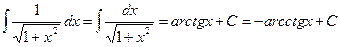 .
. 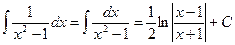 .
.
Интегрирование разложением.
Если 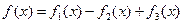 , то
, то 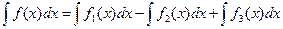 .
.
Пример 1. Найти интеграл 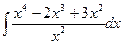 .
.
Решение.
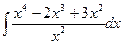 =
= 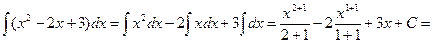
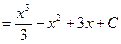 .
.
Метод подстановки.
Интегрирование путем введения новой переменной (метод подстановки) основано на формуле 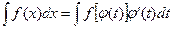 , где
, где 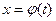 - дифференцируемая функция переменной t.
- дифференцируемая функция переменной t.
Пример 2. Найти интеграл 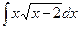 .
.
Решение. Положим 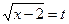 , тогда
, тогда 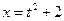 , откуда
, откуда 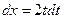 .
.
Подставляя полученные равенства в подынтегральное выражение, находим
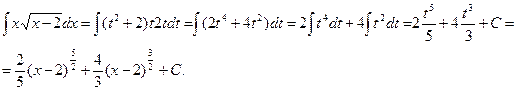
Метод интегрирования по частям.
Если 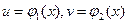 - дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций
- дифференцируемые функции от х, то из формулы для дифференциала произведения двух функций 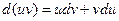 получается формула интегрирования по частям
получается формула интегрирования по частям 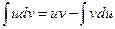 .
.
Пример 3. Найти 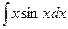 .
.
Решение. Обозначим: 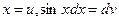 , отсюда dx = du, v = - cosx.
, отсюда dx = du, v = - cosx.
Подставляя значения u,v,du,dv в формулу интегрирования по частям, получим 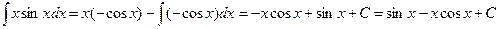 .
.
Упражнения.
4.1. Найти неопределенные интегралы:
a) 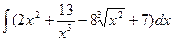 ; b)
; b) 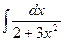 ;
;
c) 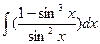 ; d)
; d) 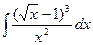 ;
;
e) 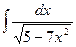 ; f)
; f) 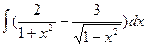 ;
;
g) 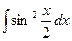 ; h)
; h) 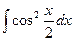 ;
;
i) 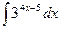 ; j)
; j) 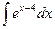 ;
;
k) 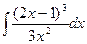 ; l)
; l) 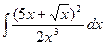 .
.
4.2. Найти неопределенные интегралы методом замены переменной:
a) 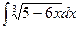 ; b)
; b) 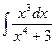 ; c)
; c) 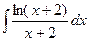 ; d)
; d) 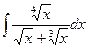 ;
;
e) 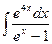 ; f)
; f) 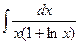 ; g)
; g) 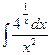 ; h)
; h) 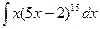 ;
;
i) 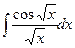 ; j)
; j) 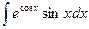 ; k)
; k) 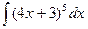 ; l)
; l) 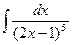 ; m)
; m) 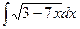
4.3. Найти неопределенные интегралы методом интегрирования по частям:
a) 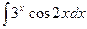 ; b)
; b) 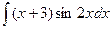 ; c)
; c) 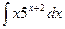 ; d)
; d) 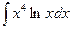 ;
;
e) 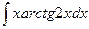 ; f)
; f) 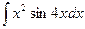 ; g)
; g) 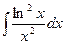 ; h)
; h) 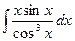 ;
;
h) 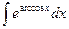 ; I)
; I) 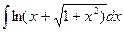 .
.
4.4. Интегрирование рациональных дробей:
a) 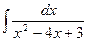 ; b)
; b) 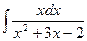 ; c)
; c) 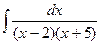 ;
;
d) 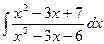 ; e)
; e) 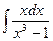 ; f)
; f) 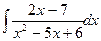 ; q)
; q) 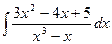 .
.
7.5. Интегрирование иррациональных выражений:
а) 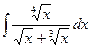 ; b)
; b) 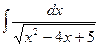 ; с)
; с) 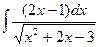 ; d)
; d) 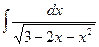 .
.
4.2 Определенный интеграл и его приложения
Определенным интегралом от функции у = f (x) на отрезке 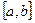 называется предел его интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю:
называется предел его интегральной суммы, когда число элементарных отрезков неограниченно возрастает, а длина наибольшего из них стремится к нулю:
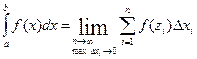 .
.
Определенным интегралом от непрерывной функции на отрезке 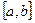 называется приращение любой его первообразной функции на этом отрезке:
называется приращение любой его первообразной функции на этом отрезке:
Формула Ньютона – Лейбница: 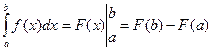 , где
, где 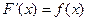 .
.
Методы вычисления определенного интеграла аналогичны вычислению неопределенного интеграла.
Замена переменной в определенном интеграле осуществляется по формуле
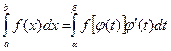 , где
, где 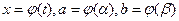 ; t – новая переменная,
; t – новая переменная, 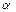 ,
, 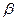 - новые пределы интегрирования.
- новые пределы интегрирования.
Интегрирование по частям в определенном интеграле:
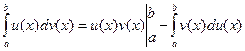 .
.
Пример 4. Вычислить определенный интеграл 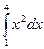 .
.
Решение. 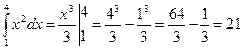 .
.
Пример 5. Вычислить 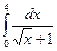 .
.
Решение. Положим 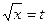 , тогда x = t2 и dx = 2tdt. Подставляя старые пределы интегрирования в формулу
, тогда x = t2 и dx = 2tdt. Подставляя старые пределы интегрирования в формулу 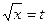 , получаем
, получаем 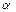 = 0,
= 0, 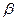 = 2.
= 2.
Следовательно
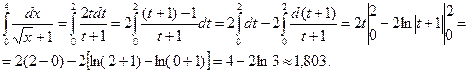
Пример 6. Вычислить 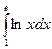 .
.
Решение. Применяем формулу интегрирования по частям. Полагая u = ln x, dv = dx, определяем 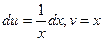 .
.
Следовательно,
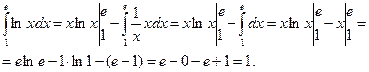
Приложения определенного интеграла
Вычисление площади плоской фигуры.
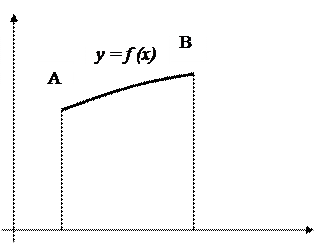
а) Площадь криволинейной трапеции АаbB, ограниченной сверху графиком кривой y = f (x), слева и справа – соответственно прямыми х = а, х = b, снизу – осью Ох, вычисляется по формуле 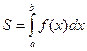 или
или 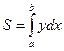 .
.
|
0 а b X
b) Площадь криволинейной фигуры, ограниченной сверху и снизу соответственно кривыми y1 = f1 (x), y2 = f2 (x), слева и справа – прямыми х = а и x = b, определяется формулой
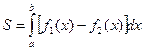 или
или 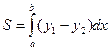 .
.
|
|
|
|
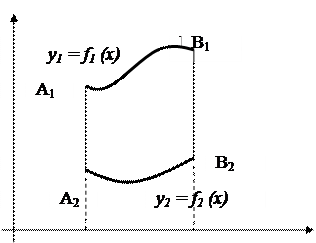
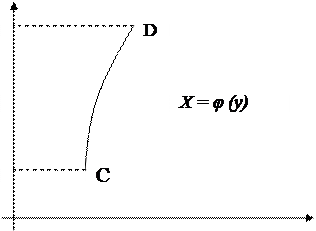
с) Площадь криволинейной трапеции, прилегающей к оси Оу, вычисляется по формуле
|
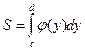 или
или 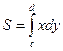 .
.
|
|
 x
x d) Если фигура расположена ниже оси OX, то
S = - 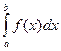
 y
y


 а в
а в
x
 |
y = f(x)
В более сложных случаях всю фигуру разбивают на части и площадь всей фигуры находят как сумму составляющих ее площадей.
Пример 7. Определить площадь фигуры, ограниченной линиями ху = 6, х = 1, х = е, у = 0.
Решение. Определяя у из уравнения гиперболы ху = 6, получим 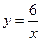 . Определим новые пределы интегрирования a = 1, b = e. Подставляя значения a, b и
. Определим новые пределы интегрирования a = 1, b = e. Подставляя значения a, b и 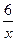 (выражение для у) в формулу, находим:
(выражение для у) в формулу, находим:
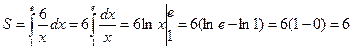 .
.
|















|
 0
0 Вычисление объема тела вращения.
Объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, где АВ – дуга кривой у = f (x), вычисляется по формуле 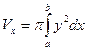 .
.
Объем тела, полученного вращением вокруг оси Оу криволинейной трапеции, где СD – дуга кривой 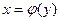 , определяется по формуле
, определяется по формуле 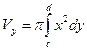 .
.
Пример 8. Найти объем тела, полученного вращением вокруг оси Ох криволинейной трапеции, ограниченной параболой у2 = 2х, прямой х = 3 и осью Ох.
Решение. В соответствии с условием задачи определяем пределы интегрирования а = 0, b = 3. Находим 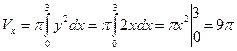 .
.
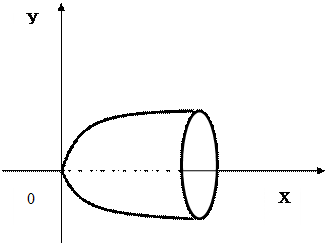
Пример 9. Найти объем тела, полученного вращением вокруг оси Оу криволинейной трапецией, ограниченной гиперболой 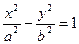 и прямыми
и прямыми 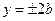 .
.
Решение. Из условия вытекает, что пределы интегрирования будут: c = - 2b, d =2b.
Выражение для х2, входящее в формулу, определяется из уравнения гиперболы:
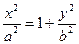 ,
, 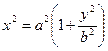 .
.
Подставляя эти выражения в формулу, получаем
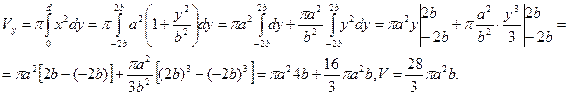
Упражнения.
4.5. Вычислить определенный интеграл:
a) 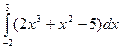 ; b)
; b)  ; c)
; c) 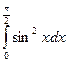 ; d)
; d) 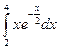 ;
;
e) 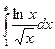 ; f)
; f) 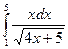 ; g)
; g) 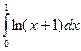 ; h)
; h) 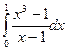 ;
;
i) 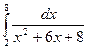 ; j)
; j) 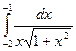 .
.
4.6. Найти площадь фигуры, ограниченной линиями. Сделать чертеж.
a) y = x2; x = 1; x = 2.
b) y2 = 4x; x = 2.
c) x = y2; y = x2 + 1; 3x + 2y – 16 = 0; x = 0.
d) y = - x2 + 4x – 1; y = - x – 1.
e) y = (x + 1)3; y2 = x + 1.
f) y3 = x; x = 1; y = 8.
g) x = 0; x = 2; y = 2x; y = 2x – x2.
i) y = 2x – x2; y = - x.
4.7 Найти объем тела, образованного вращением вокруг оси 0Х фигуры, ограниченной линиями:
a) 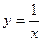 ;
; 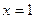 ;
; 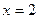 .
.
b) 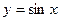 ;
; 
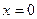 ;
; 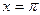 .
.
c) 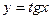 ;
; 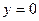 ;
; 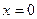 ;
; 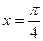 .
.
d) 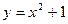 ;
; 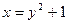 ;
; 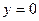 ;
; 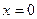 ;
; 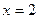 .
.
e) 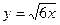 ;
; 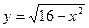 .
.
4.8 Найти объем тела, образованного вращением вокруг оси 0Y фигуры, ограниченной линиями:
a) 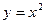 ;
; 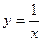 ;
; 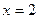 .
.
b) 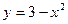 ;
; 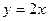 ;
; 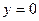 .
.
c) 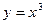 ;
; 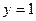 ;
; 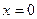 .
.
d) 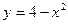 ;
; 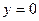 ;
; 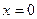 , где
, где 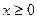 .
.
e) 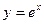 ;
; 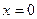 ;
; 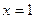 ;
; 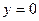 .
.
 2015-10-22
2015-10-22 2454
2454
